计算优化:Flash Attention优化#
由于核心的Attention模块计算的时空复杂度会随着序列长度的增加呈二次(平方)增长,所以Transformer结构在长序列场景计算速度慢且显存消耗较大,FlashAttention提出通过tilling / recompute的方式,减少了显存占用,加速模型训练并提升了模型效果。
标准的Attention及问题#
首先我们来简单回顾一下标准Attention的算法公式:
输入为 \(Q,K,V \in \mathbb{R}^{N \times d}\) , 其中 \(N\) 表示序列长度,\(d\) 表示注意力头的维度。在模型实际训练时,我们通常考虑通过GPU进行加速,GPU的内存由多个不同大小和不同读写速度的内存组成。以A100-40GB为例,内存分级图如下所示:
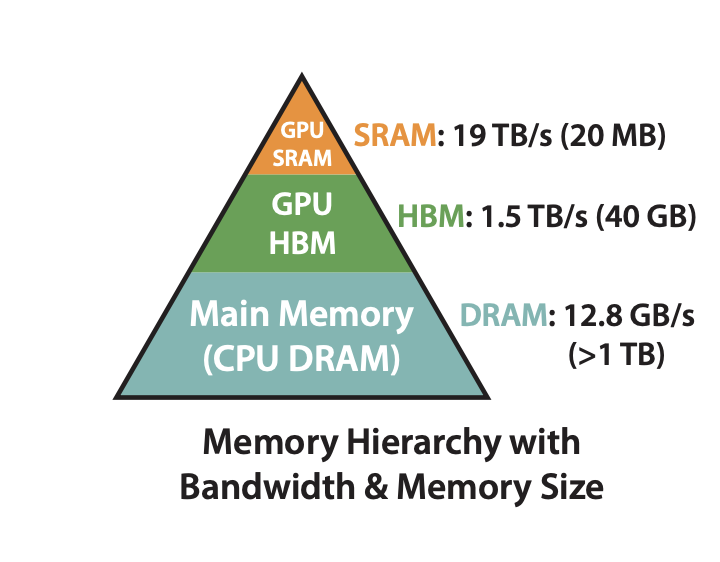
SRAM:shared memory,共20MB,带宽19TB/s
HBM:global memory,即显存,共40GB,带宽1.5TB/s
可以看到,HBM的带宽远低于SRAM的带宽。结合GPU内存分级存储架构,我们可以将标准Attention算法的实际执行过程抽象出如下流程:

计算注意力分数:首先从HBM中读取 \(Q,K\),计算 \(S=QK^\top \in \mathbb{R}^{N \times N} \) 并将结果 \(S\) 写回HBM,此时访存次数为 \(O(Nd+N^2)\)
计算注意力权重:从HBM中读取 \(S\),计算 \(P=softmax(S) \in \mathbb{R}^{N \times N} \) ,并将 \(P\) 写回HBM, 访存次数为 \(O(N^2)\)
加权求和:从HBM中读取 \(P, V\), 计算 \(O=PV\) , 并将结果 \(O\) 写回HBM, 访存次数为 \(O(Nd+N^2)\)
返回结果:返回 \(O\)
由此可见,在标准Attention的计算过程中,存在非常多对HBM的访问,同时,部分中间变量在计算完成写入HBM后又立刻被访问,如:\(S, P\),这会带来两个问题:
访存瓶颈:HBM带宽较低,频繁的HBM读写操作导致内存访问成为瓶颈,进而导致计算效率降低
显存OOM:中间变量的存储消耗大量显存空间,\(S\) 的大小为 \(N \times N\),显存占用随序列长度平方增长
为了避免中间变量S和P可能引发的低速读写以及显存压力,一个比较朴素的想法是将三个计算融合为一个算子。但是为了利用SRAM的高带宽,GEMM(通用矩阵乘法)通常需要将数据进行Tiling处理,放进SRAM中进行计算。但SRAM仅20M,当序列较长时就会被截断,从而导致标准的SoftMax无法正常工作,Flash Attention解决了这个问题。