05.GShard MOE 解读#
Author by: 张晓天
2018 年,Transformer 架构的兴起奠定了现代大语言模型的基础,但其密集特性也导致了训练与推理成本的急剧攀升。为解决此根本性挑战,条件计算(Conditional Computation)尤其是混合专家(Mixture of Experts, MoE)模型,被视为突破参数规模瓶颈的关键路径。2020 年 6 月,Google 发布论文《GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding》,首次成功地将 MoE 结构大规模、高效地应用于 Encoder-Decoder 架构的 Transformer 模型,并训练出参数量高达 6000 亿(600B)的稀疏激活模型。
本节将深入解析 GShard 的核心思想、算法创新与工程哲学,探讨其如何为后续如 Switch Transformer、GLaM 等巨型模型奠定坚实的基础。
背景与核心问题#
传统的密集 Transformer 模型在缩放(Scaling)时,所有参数都会参与每个输入样本的处理,计算成本随参数规模线性增长。MoE 模型的核心思想是稀疏激活:模型的总参数量可以极其庞大,但对于任何单个输入,仅激活其中的一个子集(即“专家”,通常为前馈网络 FFN)进行计算。
GShard 要解决的核心问题可归纳为三点:
模型规模化:如何突破硬件内存限制,稳定训练参数量远超单个设备显存容量的模型(如从十亿级到万亿级)。
计算高效性:如何在引入稀疏性的同时,确保计算和通信效率,避免因动态路由带来的系统瓶颈。
负载均衡:如何将输入令牌(Tokens)公平地分配给各专家,防止某些专家过载(成为热点)而其他专家未被充分利用(饥饿)。
模型设计#
GShard 基于Encoder-Decoder 结构的 Transformer。其关键设计在于 MoE 层的插入位置:在编码器(Encoder)和解码器(Decoder)中,每隔一层(即每两个 Transformer 层)将一个普通的 FFN 层替换为一个 MoE 层。每两层只激活 2 个 expert,但 expert 数可以飙到 2048,从而把参数撑到 600B,而计算量几乎不变。
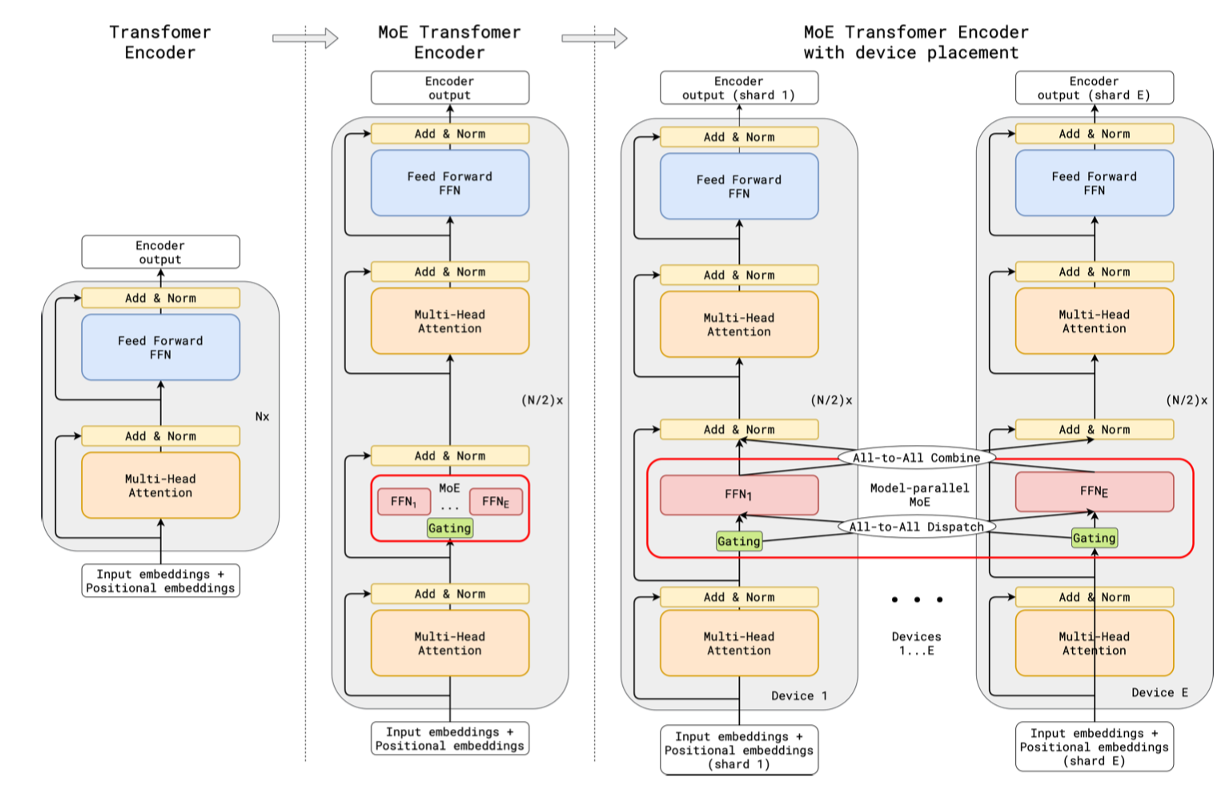
对于一个总层数为 N 的模型,其中包含 N/2 个 MoE 层。这种设计在引入大量稀疏参数(主要存在于 MoE-FFN 中)的同时,保留了足够多的共享稠密层(如注意力层、剩余的 FFN 层),保证了模型的表示能力和稳定性。
专家结构与门控网络#
专家(Expert):每个专家本身就是一个标准的 FFN(如具有扩展维度的两层全连接网络)。模型总参数量随专家数量(E)线性增长。
门控函数(Gating Function):对于每个输入令牌,门控网络GATE(x)计算其与所有专家匹配的权重,并据此进行路由。GShard 的门控函数设计遵循两大原则:负载均衡与高效扩展。
GShard 在门控函数的设计上提出了两个要求:
(1)负载均衡
(2)高效扩展。
负载均衡和前面讲的一样,很好理解。而为什么要高效扩展,因为如果要对 N 个 token 分别进行 E 个 expert 的分配,在 N 能达到百万甚至千万级别,而 E 也有几百上千的情况下,就需要一个高效的分布式实现,以免其他计算资源等待门控函数。
Top-2 路由与随机路由机制#
GShard 采用Top-2 门控。即每个令牌x会选择权重最高的前两位专家(expert1, expert2),而非仅选择 Top-1。这样做有两个好处:
增加冗余与鲁棒性:为模型提供一定的容错能力,即使某个专家表现不佳,仍有另一个专家作为补充。
便于负载均衡:通过调整两个专家的流量,更容易实现均衡分配。
然而,并非所有 Top-2 专家都会被无条件激活。GShard 引入了一项精妙的随机路由(Random Routing) 机制:
Top-1 专家总是被激活。
Top-2 专家是否被激活,则依概率进行。具体而言,以第二个专家的门控权重
g2为概率来决定是否激活它。如果g2很小,则它很可能被忽略。 这种机制在保持模型容量的同时,显著降低了计算和通信开销,因为它有效地减少了需要实际处理的专家数量,尤其避免了为大量权重极低的专家分配计算资源。
专家容量与分组负载均衡#
这是 GShard 解决负载均衡和系统效率问题的核心方案。
专家容量(Expert Capacity)#
为了绝对防止单个专家过载,GShard 设定了一个硬性限制:每个专家最多能处理的令牌数量上限,即专家容量(Capacity),记为C。论文中将其设置为C = (2 * N) / E,其中 N 是批次中的令牌总数,E 是专家总数。这意味着即使负载极端不均衡,系统也最多允许专家处理两倍于平均负载的令牌量。
令牌缓冲机制:门控网络为每个专家维护一个计数器。当一个令牌被路由至某个专家时,该专家的计数器加 1。如果该专家当前已处理的令牌数已达到其容量C,则即使该令牌的门控权重很高,也会被拒绝。这些被拒绝的令牌不会由该 MoE 层中的任何专家处理,而是直接通过残差连接绕过该层,传递至下一层。这确保了前向传播的顺利进行。
分组(Grouping)与自动分片(Automatic Sharding)#
这是 GShard 工程实现的精髓,也是其名称的由来。
分组:将输入的一个大批次(Large Batch)的令牌在序列维度上划分为
G个更小的组(Groups)。每个组独立地进行门控计算和专家分配。**每个组内的专家容量相应地变为(2 * N) / (E * G)。好处:
降低通信开销:最重要的好处在于,后续所需的 All-to-All 通信(用于将不同令牌发送到其对应专家所在的设备)只需在每个组内部进行。通信量从全局规模降至组内规模,极大地提升了扩展性。
兼容梯度累积:在反向传播时,这些组可以合并起来一起计算梯度,这等价于进行了梯度累积(Gradient Accumulation),保持了训练的有效批次大小(Effective Batch Size)不变。
通过“分组”和“专家容量”这两个设计,GShard 将动态且不可预测的稀疏计算,转换为了一个具有已知且固定计算与通信预算的准静态操作,从而使得大规模分布式训练成为可能。
小结#
GShard 是一项里程碑式的工作,它不仅在算法层面创新地提出了 Top-2 随机路由、专家容量等机制,更在工程层面通过分组(Grouping)和自动分片技术,首次实现了在通用硬件上高效训练万亿参数级别的稀疏模型。
其影响深远:
技术路线:它奠定了现代 MoE Transformer 的基础架构和设计范式,后续的如 Switch Transformer(采用更极端的 Top-1 路由)、GLaM 等模型均直接受其启发。
工程范式:它证明了通过精巧的系统设计与算法协同优化,可以突破硬件的绝对限制,开启了一个“规模远超内存”的模型训练新纪元。
GShard 清晰地指出:未来的 AI 发展不仅是算法的革新,更是算法与系统工程深度协同设计(Co-Design) 的胜利。