Ulysses 长序列并行#
Author by: 付溦崴
DeepSpeed 提出了一种新的序列并行方法:DeepSpeed-Ulysses。 在 Transformer 结构中,**前馈层(FFN)**的计算是逐 token 独立的,不依赖于序列长度。而 自注意力机制(Self-Attention) 则不同,它需要全局的信息交互:每个 Query 都必须与整个序列的 Key、Value 交互。
因此,Attention 的计算是序列并行的最大挑战:
序列被分割后,每张 GPU 只持有部分 token,无法单独完成注意力计算。
必须通过 通信操作 在 GPU 之间交换 Q/K/V,确保每个 GPU 能看到完整的序列。
传统的 Megatron-LM 序列并行方案通过 AllGather 等通信完成这一过程,但其通信复杂度较高,扩展性有限。DeepSpeed-Ulysses 的核心贡献就是降低序列并行的通信量,从而支持更长的序列。
DeepSpeed-Ulysses 整体流程#
简单来说 Ulysses 的核心思想是:
利用两次 All-to-All,将数据重分布,使得每个 GPU 既能并行处理子序列,又能独立计算完整的 Attention Head。
整体的流程如下图所示:
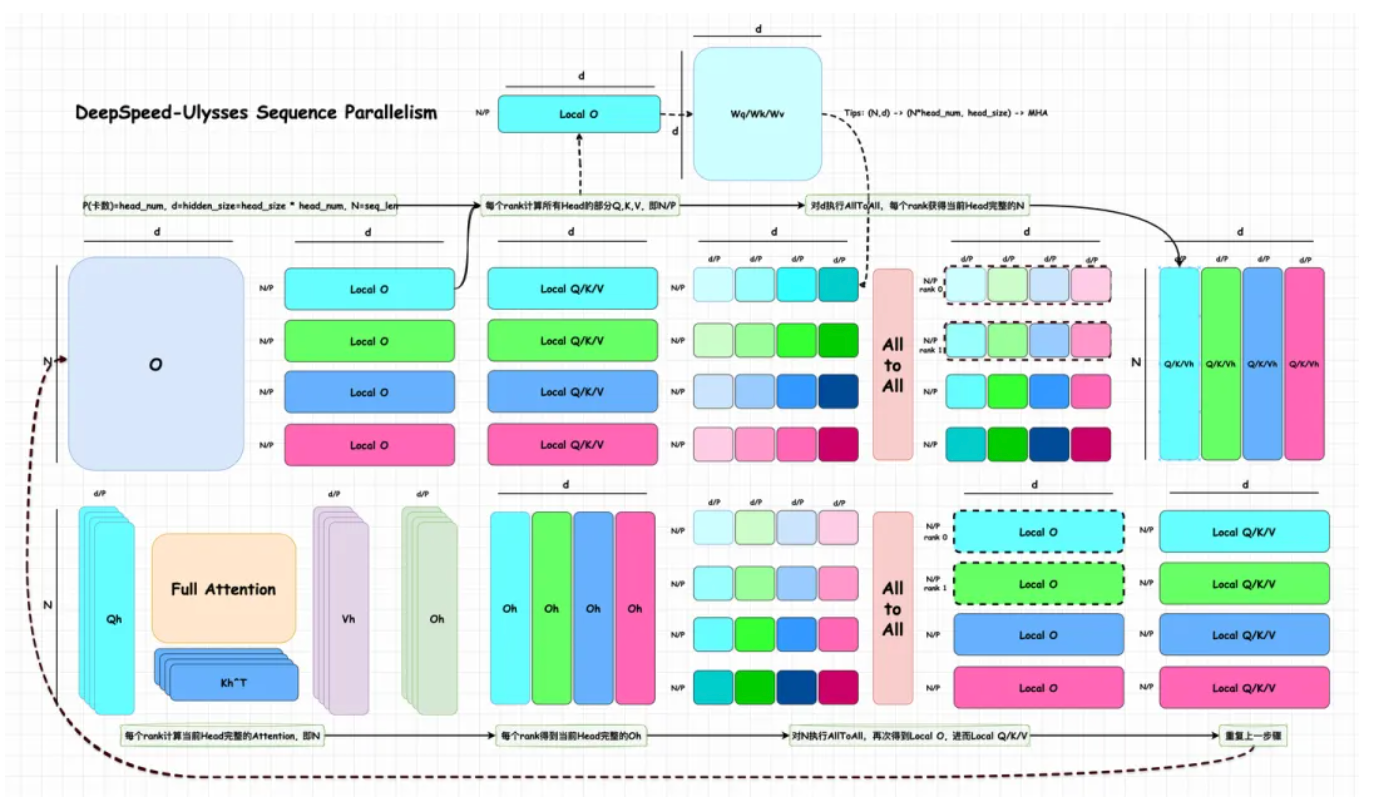
我们可以假设 GPU 数量为 P,注意力头数为 head num,满足 head_num % P=0,这里为了简化理解,我们假设 P = head num。图中,Local O/Q/K/V 表示每个 rank 上的数据,Qh, Kh, Vh, Oh 表示当前 head 上在 N 维度上完整的数据。N 表示序列长度 seq len,d 表示 hidden size,head size 表示每个注意力头使用的隐藏向量的维度,并且满足:d=hidden_size=head_size * head_num。P 和 head num 应该需要满足整除关系,从另一方面来看,其实也保证 MHA 计算的数值正确性,每个 Head 本身的 hd 维度需要完整,才能保证 Attention score 是数值正确的。因此,Ulysses 图中的 d/P,实际上只是按照 head num 进行切分,并不会对每个 head 自身的 hd 再次切分。
输入矩阵切分: 首先,对输入矩阵 O 进行切分,每个卡上获得[N/P,d]大小分块的数据,即 Local O。DeepSpeed-Ulysses 不对权重进行切分,每个卡上持有完整的 Wq/Wk/Wv 权重。因此,每个卡上的[N/P,d]分块,可以直接和当前卡上的 Wq/Wk/Wv 相乘,得到[N/P,d]大小的 Q,K,V 矩阵作为输出,即 Local Q/K/V。注意,这些 Q,K,V 矩阵的性质是:所有 Head 的部分 Q, K, V,即 N/P。
第一次 All-to-All(对 d 维度): 经过上一个步骤,我们得到的 Local Q/K/V,每个卡只有持有其中 N/P 部分,但是 Attention 部分要求对完整的 N 进行注意力机制的计算,并且,最好同时能实现 Attention 的分布式运算。为此,我们需要使得每卡恰好持有一个 Attention Head 的 N 维度上完整的 Q/K/V 值。这要怎么实现呢?DeepSpeed 团队发现,此时,只要对 d 维度执行一个 All-To-All 操作,恰好能实现这个功能。
All-To-All 这个通信方式同 All-Reduce 一样,是分布式训练中的 Collective functions,All-to-All 在每个进程向每个其他进程发消息的一部分,最后处理器拥有各个进程消息的一部分,这个操作可以理解成一个分布式矩阵转置操作。以下图为例,执行 All-To-All 后,rank 0 持有 4 个[N/P, d/P]的数据,分别属于 N 的不同部分,因此可以进一步合并成[N, d/P=head_size]。这正好是一个 head 所需要的在 N 维度上完整的 Q/K/V。
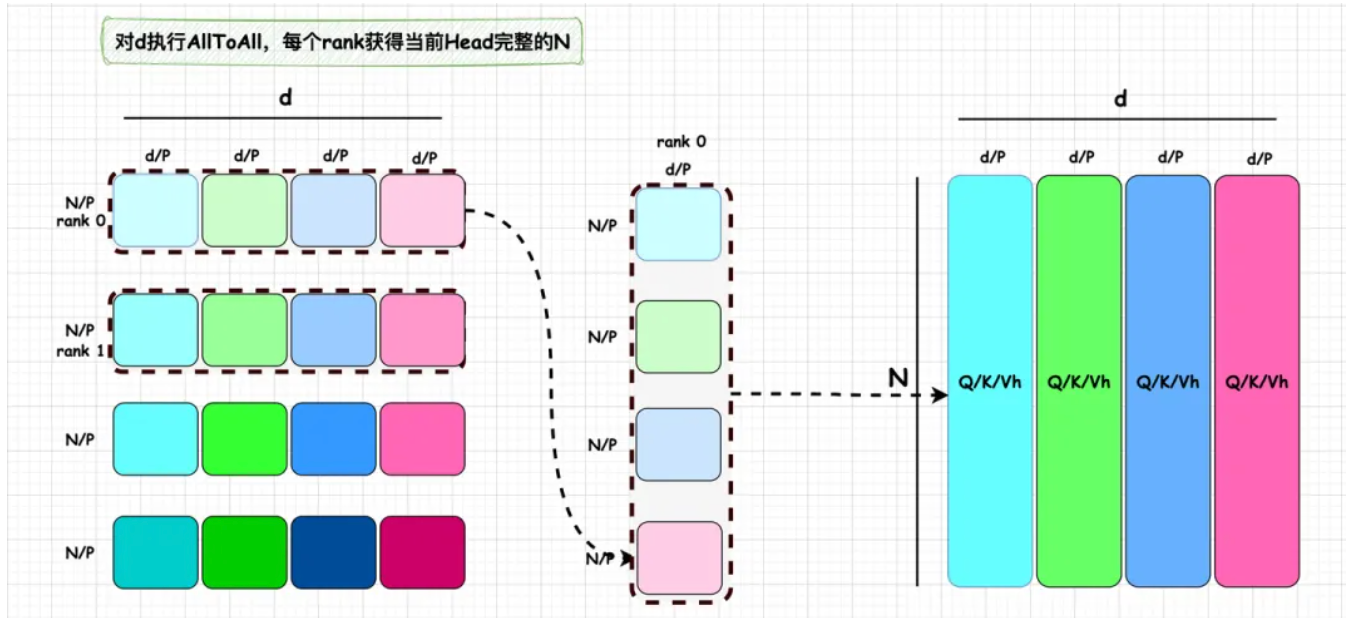
Attention 计算: 由于经过 All-To-All 后,每个 rank 都恰好拿到了一个 head 在 N 维度上完整的 Q/K/V,即 Qh, Kh 和 Vh,因此可以按照正常的 Attention 流程进行注意力机制计算,每个 rank 得到当前 Head 完整的 Oh。
第一次 All-to-All(对 N 维度): 每个 rank 得到当前 Head 完整的 Oh 后,为了能够使得后续的和 Wo 相乘以及 MLP 模块能够直接执行序列并行,我们还需要将 Oh([N, d/P])变换成 Local O([N/P, d])的形式,而这恰好又可以用另一个 All-To-All 来完成,即,对 N 维度执行 All-To-All。得到的结果恰好就是 Local O 的形式,那么,可以直接把结果传给 Wo 以及 MLP,继续执行序列并行。
-MLP 计算:这部分计算就如上述所说,每个 token 的计算是独立的,因此可以在不同卡上进行分块计算。
下图对 Megatron-LM SP+DP 的训练性能对比:
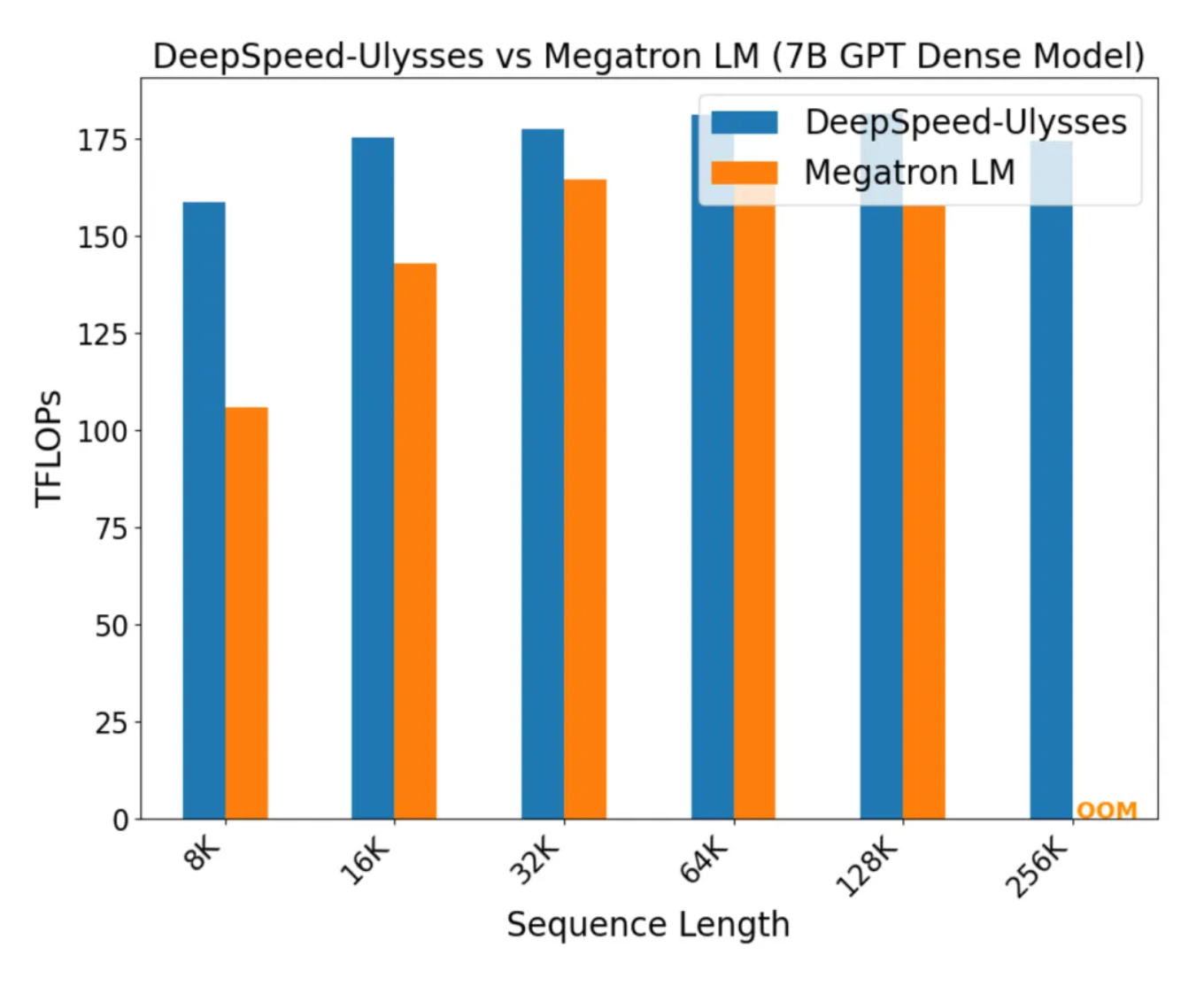
通信量分析#
All-to-All 的通信量#
在执行 All-to-All 操作之前,每张 GPU 保存的数据规模为:\( \frac{N \cdot d}{P} \)
其中,\(N\) 为序列长度,\(d\) 为隐藏层维度,\(P\) 为并行度(GPU 数量)。
进一步切分后,每个小数据块的大小为:\( \frac{N \cdot d}{P^2} \)
在 All-to-All 通信中,单卡既要 发送(send) 数据,也要 接收(accept) 数据。但从通信量角度,可以将系统的总通信量理解为所有 GPU 的发送量之和,因此单卡的通信量只需关注 send 部分。
对于单卡而言,它的发送量为:
\( \text{send} = \frac{N \cdot d}{P^2} \times (P-1) \)
当 \(P\) 较大时,约等于:
\( \frac{N \cdot d}{P} \)
也就是说,单卡执行一次 All-to-All 的通信量大约是 \( \frac{N \cdot d}{P} \)。
相比之下,单卡执行一次 All-Gather 或 Reduce-Scatter 的通信量则是 \( N \cdot d \)。这表明 All-to-All 的通信量被有效地降低了一个数量级。
Forward 通信量#
q/k/v_chunk 各自做 1 次 All-to-All 通讯,则这里合起来做了 3 次 All-to-All 通讯,各卡上原始的 Attention 结果做了 1 次 All-to-All 通讯综上,Ulysses 的前向过程一共做了 4 次 All-to-All 通讯,因此总通信量为 \(\frac{4Nd}{P}\)。 (注意,如果配套使用了 zero 操作,fwd 过程还会涉及模型权重的 all-gather,不过这里我们不考虑这一点,我们就假设是最朴素的 ulysses,单卡上有完整的模型)
下面的表格对比了 Ulysses 与 Megatron-LM SP 的通信量:
特性 |
DeepSpeed-Ulysses |
Megatron-LM SP |
|---|---|---|
切分方式 |
序列维度 + Head 维度重分布 |
序列维度 |
通信模式 |
双 All-to-All(d + N) |
AllGather/AllReduce |
通信复杂度 |
\(O(N/P)\) |
\(O(N)\) |
扩展性 |
更适合超长序列 |
较难扩展到百万级别 |
工程实现 |
与 ZeRO/FlashAttention 等兼容 |
强绑定 TP,更复杂 |