CODE 03: MFU 模型利用率评估

CODE 03: MFU 模型利用率评估#

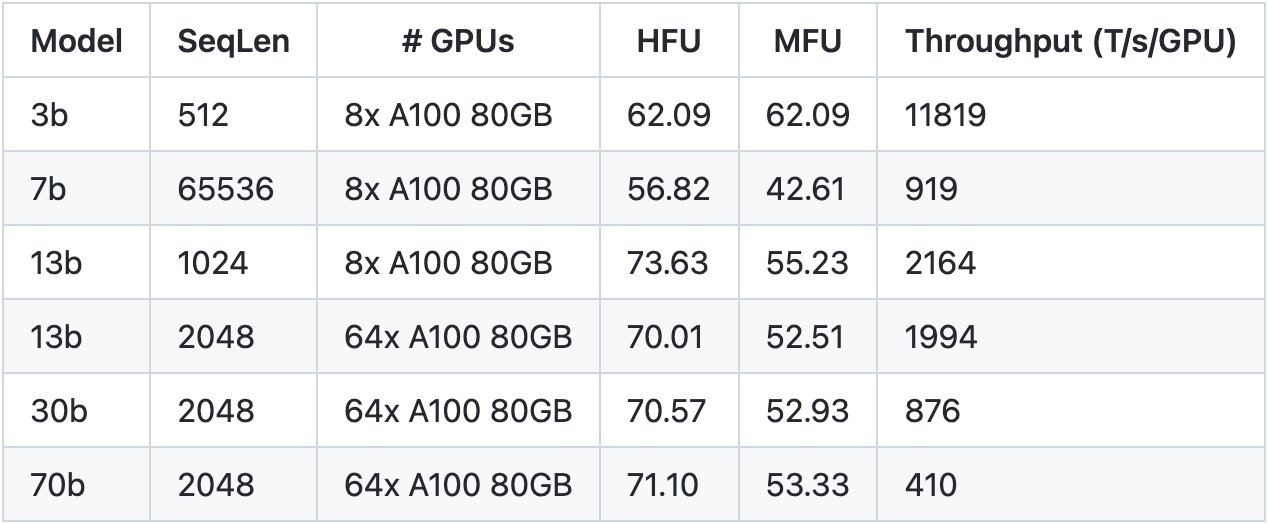
模型算力利用率（Model FLOPs Utilization, MFU）是评估 AI 模型训练效率的关键指标，它衡量了模型在实际训练中对硬件计算能力的利用程度。

其计算公式为：

\[ \text{MFU} = \frac{\text{模型实际 FLOPs/迭代时间}}{\text{硬件峰值 FLOPs}} = \frac{\text{实际 FLOPS}}{\text{理论 FLOPS}} \]

要准确计算 MFU，关键在于精确计算模型的 FLOPs。下面我们将分别推导稠密 Transformer 和 MoE 架构的计算公式。

2. 稠密 Transformer 的计算量#

2.1 自注意力机制 FLOPs 计算#

对于单头注意力，计算过程可分为三个部分：

  1. Q、K、V 投影： $\( \text{FLOPs}_{\text{proj}} = 3 \times B \times s \times h \times h \times 2 = 6Bs h^2 \)$

  2. 注意力计算（QK^T 和 softmax）： $\( \text{FLOPs}_{\text{attn}} = B \times n_{\text{heads}} \times (2 \times s \times h_{\text{per\_head}} \times s) = 2Bs^2 h \)$

  3. 输出投影： $\( \text{FLOPs}_{\text{out}} = B \times s \times h \times h \times 2 = 2Bs h^2 \)$

2.2 MLP FLOPs 计算#

标准 FFN 包含两个线性变换和激活函数：

\[ \text{FLOPs}_{\text{mlp}} = B \times s \times (2 \times h \times 4h + 2 \times 4h \times h) = 16Bs h^2 \]

2.3 嵌入层 FLOPs 计算#

\[ \text{FLOPs}_{\text{embed}} = B \times s \times h \times V \times 2 = 2Bs h V \]

2.4 完整稠密模型 FLOPs 公式#

综合所有组件，单次前向传播的 FLOPs 为：

\[ \text{FLOPs}_{\text{forward}} = L \times (6Bs h^2 + 2Bs^2 h + 2Bs h^2 + 16Bs h^2) + 2Bs h V \]

简化后：

\[ \text{FLOPs}_{\text{forward}} = 24L Bs h^2 + 2L Bs^2 h + 2Bs h V \]

考虑反向传播（计算量约为前向的 2 倍），总 FLOPs 为：

\[ \text{FLOPs}_{\text{total}} = 3 \times (24L Bs h^2 + 2L Bs^2 h + 2Bs h V) \]
\[ \text{FLOPs}_{\text{total}} = 72L Bs h^2 + 6L Bs^2 h + 6Bs h V \]

3. MoE 架构的 FLOPs 计算#

3.1 MoE 架构的特殊性#

MoE（Mixture of Experts）模型的关键特点：

  • 总专家数：\(E_{\text{total}}\)

  • 每个 token 激活的专家数：\(E_{\text{active}}\)（通常为 1-2）

  • 门控网络计算开销

3.2 注意力部分 FLOPs#

\[ \text{FLOPs}_{\text{attn}} = 72L Bs h^2 + 6L Bs^2 h \]

3.3 MLP 部分 FLOPs#

\[ \text{FLOPs}_{\text{mlp-moe}} = 16L Bs h^2 \times \frac{E_{\text{active}}}{E_{\text{total}}} \]

3.4 门控网络 FLOPs#

\[ \text{FLOPs}_{\text{gate}} = 2L Bs h E_{\text{total}} \]

3.5 嵌入层 FLOPs#

\[ \text{FLOPs}_{\text{embed}} = 6Bs h V \]

3.6 完整 MoE 模型 FLOPs#

\[ \text{FLOPs}_{\text{moe-total}} = 72L Bs h^2 + 6L Bs^2 h + 16L Bs h^2 \times \frac{E_{\text{active}}}{E_{\text{total}}} + 2L Bs h E_{\text{total}} + 6Bs h V \]

4. FLOPs 计算函数#

def compute_dense_flops(L, h, B, s, V, include_backward=True):
    """
    计算稠密 Transformer 模型的 FLOPs
    
    参数:
    L: Transformer 层数
    h: 隐藏层维度
    B: 批次大小
    s: 序列长度
    V: 词表大小
    include_backward: 是否包含反向传播
    
    返回:
    total_flops: 总 FLOPs 数
    """
    # 前向传播 FLOPs
    flops_forward = (
        24 * L * B * s * h**2 +  # 注意力机制和 MLP 的主要计算
        2 * L * B * s**2 * h +   # 注意力矩阵计算
        2 * B * s * h * V        # 嵌入层
    )
    
    # 总 FLOPs（前向+反向）
    coeff = 3 if include_backward else 1
    total_flops = coeff * flops_forward
    
    return total_flops

def compute_moe_flops(L, h, B, s, V, E_total, E_active=2, include_backward=True):
    """
    计算 MoE Transformer 模型的 FLOPs
    
    参数:
    L: Transformer 层数
    h: 隐藏层维度
    B: 批次大小
    s: 序列长度
    V: 词表大小
    E_total: 总专家数
    E_active: 每个 token 激活的专家数
    include_backward: 是否包含反向传播
    
    返回:
    total_flops: 总 FLOPs 数
    """
    # 注意力部分 FLOPs（与稠密模型相同）
    flops_attn = 72 * L * B * s * h**2 + 6 * L * B * s**2 * h
    
    # MoE 特有的 MLP 部分 FLOPs
    flops_mlp_moe = 16 * L * B * s * h**2 * (E_active / E_total)
    
    # 门控网络 FLOPs
    flops_gate = 2 * L * B * s * h * E_total
    
    # 嵌入层 FLOPs
    flops_embed = 6 * B * s * h * V
    
    # 总 FLOPs
    total_flops = flops_attn + flops_mlp_moe + flops_gate + flops_embed
    
    return total_flops

让我们通过具体数值来计算 DeepSeek 和 Qwen3 的 FLOPs。

# DeepSeek-7B 参数配置
L_deepseek = 30    # 层数
h_deepseek = 4096  # 隐藏维度
V_deepseek = 102400  # 词表大小

# Qwen3-7B 参数配置
L_qwen = 40        # 层数
h_qwen = 5120      # 隐藏维度
V_qwen = 151936    # 词表大小

# 训练配置
B = 4      # 批大小
s = 512    # 序列长度

# 计算稠密模型 FLOPs
flops_deepseek_dense = compute_dense_flops(L_deepseek, h_deepseek, B, s, V_deepseek)
flops_qwen_dense = compute_dense_flops(L_qwen, h_qwen, B, s, V_qwen)

print(f"DeepSeek 稠密模型 FLOPs/迭代: {flops_deepseek_dense / 1e12:.2f} TFLOPs")
print(f"Qwen3 稠密模型 FLOPs/迭代: {flops_qwen_dense / 1e12:.2f} TFLOPs")

# 计算 MoE 模型 FLOPs（假设 8 个专家，激活 2 个）
E_total = 8
E_active = 2

flops_deepseek_moe = compute_moe_flops(L_deepseek, h_deepseek, B, s, V_deepseek, E_total, E_active)
flops_qwen_moe = compute_moe_flops(L_qwen, h_qwen, B, s, V_qwen, E_total, E_active)

print(f"DeepSeek-MoE 模型 FLOPs/迭代: {flops_deepseek_moe / 1e12:.2f} TFLOPs")
print(f"Qwen3-MoE 模型 FLOPs/迭代: {flops_qwen_moe / 1e12:.2f} TFLOPs")

# 计算 MoE 相对于稠密的节省比例
saving_deepseek = (flops_deepseek_dense - flops_deepseek_moe) / flops_deepseek_dense
saving_qwen = (flops_qwen_dense - flops_qwen_moe) / flops_qwen_dense

print(f"DeepSeek-MoE FLOPs 节省: {saving_deepseek * 100:.2f}%")
print(f"Qwen3-MoE FLOPs 节省: {saving_qwen * 100:.2f}%")

5. MFU 计算完整实现#

def calculate_mfu_comprehensive(model_config, batch_size, seq_length, iteration_time, device_flops, is_moe=False):
    """
    综合计算模型的 MFU
    
    参数:
    model_config: 模型配置字典
    batch_size: 批次大小
    seq_length: 序列长度
    iteration_time: 迭代时间(秒)
    device_flops: 设备峰值 FLOPS
    is_moe: 是否为 MoE 模型
    
    返回:
    mfu: 模型算力利用率
    detailed_breakdown: 详细计算分解
    """
    # 提取模型参数
    L = model_config['num_hidden_layers']
    h = model_config['hidden_size']
    V = model_config['vocab_size']
    
    if is_moe:
        E_total = model_config.get('num_experts', 8)
        E_active = model_config.get('num_experts_per_tok', 2)
        total_flops = compute_moe_flops(L, h, batch_size, seq_length, V, E_total, E_active)
    else:
        total_flops = compute_dense_flops(L, h, batch_size, seq_length, V)
    
    # 计算实际 FLOPS
    actual_flops_per_sec = total_flops / iteration_time
    
    # 计算 MFU
    mfu = actual_flops_per_sec / device_flops
    
    # 生成详细分解
    detailed_breakdown = {
        'total_flops': total_flops,
        'iteration_time': iteration_time,
        'actual_flops_per_sec': actual_flops_per_sec,
        'device_flops': device_flops,
        'mfu': mfu
    }
    
    return mfu, detailed_breakdown

让我们通过具体数值来分析不同架构的 MFU 差异。

# 设备峰值算力（假设 A100 GPU）
device_flops = 312 * 1e12  # 312 TFLOPS

# 模型配置
deepseek_config = {
    'num_hidden_layers': 30,
    'hidden_size': 4096,
    'vocab_size': 102400
}

qwen_config = {
    'num_hidden_layers': 40,
    'hidden_size': 5120,
    'vocab_size': 151936
}

# 假设的迭代时间（基于实际测量）
iteration_time_dense = 0.5  # 秒
iteration_time_moe = 0.3    # 秒

# 计算 MFU
print("DeepSeek 模型 MFU 分析:")
mfu_deepseek_dense, breakdown_dense = calculate_mfu_comprehensive(
    deepseek_config, 4, 512, iteration_time_dense, device_flops, False
)
mfu_deepseek_moe, breakdown_moe = calculate_mfu_comprehensive(
    deepseek_config, 4, 512, iteration_time_moe, device_flops, True
)

print(f"稠密架构 MFU: {mfu_deepseek_dense * 100:.2f}%")
print(f"MoE 架构 MFU: {mfu_deepseek_moe * 100:.2f}%")
print(f"MFU 提升: {(mfu_deepseek_moe - mfu_deepseek_dense) / mfu_deepseek_dense * 100:.2f}%")

# 输出详细计算信息
print("\n 详细计算分解（稠密）:")
for key, value in breakdown_dense.items():
    if 'flops' in key:
        print(f"{key}: {value / 1e12:.2f} TFLOPs")
    else:
        print(f"{key}: {value}")

print("\n 详细计算分解（MoE）:")
for key, value in breakdown_moe.items():
    if 'flops' in key:
        print(f"{key}: {value / 1e12:.2f} TFLOPs")
    else:
        print(f"{key}: {value}")

不同条件下的 MFU 分析

def analyze_mfu_variations(model_config, device_flops, is_moe=False):
    """
    分析不同批大小和序列长度对 MFU 的影响
    
    参数:
    model_config: 模型配置
    device_flops: 设备峰值 FLOPS
    is_moe: 是否为 MoE 模型
    """
    import matplotlib.pyplot as plt
    import numpy as np
    
    # 测试不同的批大小和序列长度
    batch_sizes = [1, 2, 4, 8, 16]
    seq_lengths = [256, 512, 1024, 2048]
    
    # 假设迭代时间与计算量成正比
    base_time = 0.3 if is_moe else 0.5
    
    results = np.zeros((len(batch_sizes), len(seq_lengths)))
    
    for i, bs in enumerate(batch_sizes):
        for j, sl in enumerate(seq_lengths):
            # 估算迭代时间（与实际计算量成正比）
            if is_moe:
                flops = compute_moe_flops(
                    model_config['num_hidden_layers'],
                    model_config['hidden_size'],
                    bs, sl,
                    model_config['vocab_size'],
                    8, 2
                )
            else:
                flops = compute_dense_flops(
                    model_config['num_hidden_layers'],
                    model_config['hidden_size'],
                    bs, sl,
                    model_config['vocab_size']
                )
            
            # 假设迭代时间与 FLOPs 成正比
            iteration_time = base_time * (flops / (312 * 1e12))  # 归一化
            
            mfu, _ = calculate_mfu_comprehensive(
                model_config, bs, sl, iteration_time, device_flops, is_moe
            )
            results[i, j] = mfu
    
    # 可视化结果
    plt.figure(figsize=(12, 5))
    
    # 批大小对 MFU 的影响
    plt.subplot(1, 2, 1)
    for j, sl in enumerate(seq_lengths):
        plt.plot(batch_sizes, results[:, j], 'o-', label=f'SeqLen={sl}')
    plt.xlabel('Batch Size')
    plt.ylabel('MFU')
    plt.title('MFU vs Batch Size')
    plt.legend()
    plt.grid(True)
    
    # 序列长度对 MFU 的影响
    plt.subplot(1, 2, 2)
    for i, bs in enumerate(batch_sizes):
        plt.plot(seq_lengths, results[i, :], 'o-', label=f'BS={bs}')
    plt.xlabel('Sequence Length')
    plt.ylabel('MFU')
    plt.title('MFU vs Sequence Length')
    plt.legend()
    plt.grid(True)
    
    plt.tight_layout()
    plt.show()
    
    return results

6. 技术原理深度解析#

MoE 架构的核心思想是通过稀疏激活来减少计算量：

\[ \text{计算节省} = 1 - \frac{E_{\text{active}}}{E_{\text{total}}} \]

当 \(E_{\text{total}} = 8\) 且 \(E_{\text{active}} = 2\) 时，MLP 部分的计算量减少到原来的 25%。

实际 MFU 通常低于理论值的主要原因：

  1. 内存带宽限制：数据搬运时间占比较大

  2. 通信开销：分布式训练中的梯度同步

  3. 计算并行度：无法完全利用所有计算单元

  4. 内核启动开销：GPU 内核启动的延迟

\[ \text{实际 MFU} = \text{理论 MFU} \times \eta_{\text{memory}} \times \eta_{\text{communication}} \times \eta_{\text{parallelism}} \]

7. 总结与思考#

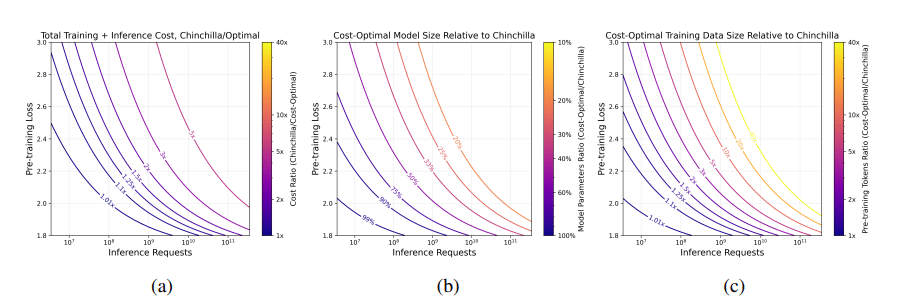
通过公式推导和代码实现，我们深入分析了稠密和 MoE 架构的 FLOPs 计算原理。稀疏激活，MoE 架构可以显著减少计算量，通常能节省 50-75%的 FLOPs，虽然 MoE 减少计算量，但需要权衡通信开销和内存使用。

另外，为了提高 MFU 需要综合考虑计算、内存、通信三个方面的综合优化。

本节目录 Contents