CODE 04: 专家并行大规模训练#
本实验旨在深入理解混合专家模型(MoE)架构中的专家并行技术，掌握大规模模型训练的基本原理，并实践权重转换技术。通过简化但完整的代码实现，帮助初学者理解 MoE 架构的核心概念和实现方法。
1. MoE 模型原理#
MoE 模型是一种将多个"专家"网络组合成一个大型模型的技术。每个专家是一个相对较小的神经网络，专门处理特定类型或特定分布的数据。MoE 的核心思想是通过一个门控网络(gating network)来决定每个输入应该被路由到哪些专家进行处理。
在 MoE 中，前向传播可以表示为：
\[y = \sum_{i=1}^{n} G(x)_i \cdot E_i(x)\]
其中：
\(E_i\) 是第 i 个专家网络
\(G(x)_i\) 是门控网络对于第 i 个专家的输出权重
\(n\) 是专家数量
门控网络通常使用 softmax 函数确保所有权重之和为 1：
\[G(x) = \text{softmax}(W_g \cdot x + b_g)\]
2. 基础 MoE 层实现#
首先，我们实现一个基础的 MoE 层，包含多个专家和一个门控网络。
import torch
import torch.nn as nn
import torch.nn.functional as F
class BasicMoELayer(nn.Module):
"""
基础 MoE 层实现
包含多个专家网络和一个门控网络
"""
def __init__(self, input_size, output_size, num_experts, expert_hidden_size=64):
super().__init__()
self.input_size = input_size
self.output_size = output_size
self.num_experts = num_experts
# 创建专家网络 - 每个专家是一个简单的 MLP
self.experts = nn.ModuleList([
nn.Sequential(
nn.Linear(input_size, expert_hidden_size),
nn.ReLU(),
nn.Linear(expert_hidden_size, output_size)
) for _ in range(num_experts)
])
# 门控网络 - 决定输入如何分配给专家
self.gate = nn.Linear(input_size, num_experts)
def forward(self, x):
"""
前向传播过程
1. 门控网络计算每个专家的权重
2. 选择 top-k 专家
3. 计算专家输出并加权组合
"""
# 计算门控权重
gate_scores = self.gate(x)
gate_probs = F.softmax(gate_scores, dim=-1)
# 选择 top-2 专家
top2_probs, top2_indices = torch.topk(gate_probs, k=2, dim=-1)
# 归一化选中的专家权重
top2_probs = top2_probs / top2_probs.sum(dim=-1, keepdim=True)
# 计算最终输出（修正：初始化时指定设备，与输入保持一致）
final_output = torch.zeros(x.size(0), self.output_size, device=x.device)
# 对每个选中的专家计算输出并加权组合
for i in range(2):
expert_idx = top2_indices[:, i]
expert_mask = torch.zeros_like(gate_probs)
# 创建专家掩码
for j in range(x.size(0)):
expert_mask[j, expert_idx[j]] = 1
# 计算当前专家组的输出
expert_outputs = []
for idx in range(self.num_experts):
expert_input = x[expert_mask[:, idx].bool()]
if expert_input.size(0) > 0:
# 修正原代码中的语法错误：self.expertsexpert_input → self.experts[idx](expert_input)
expert_out = self.experts[idx](expert_input)
expert_outputs.append((expert_out, expert_mask[:, idx].bool()))
# 组合专家输出
for expert_out, mask in expert_outputs:
final_output[mask] += expert_out * top2_probs[mask, i].unsqueeze(1)
return final_output
# 测试基础 MoE 层
input_size = 10
output_size = 5
num_experts = 4
batch_size = 8
moe_layer = BasicMoELayer(input_size, output_size, num_experts)
x = torch.randn(batch_size, input_size)
output = moe_layer(x)
print(f"输入形状: {x.shape}")
print(f"输出形状: {output.shape}")
print(f"MoE 层参数数量: {sum(p.numel() for p in moe_layer.parameters())}")
输入形状: torch.Size([8, 10])
输出形状: torch.Size([8, 5])
MoE 层参数数量: 6973
这个基础 MoE 层实现展示了 MoE 模型的核心概念。每个专家是一个独立的小型神经网络，门控网络决定输入如何分配给不同的专家。在实际应用中，MoE 可以显著增加模型容量而不显著增加计算成本，因为每个输入只使用少数专家。
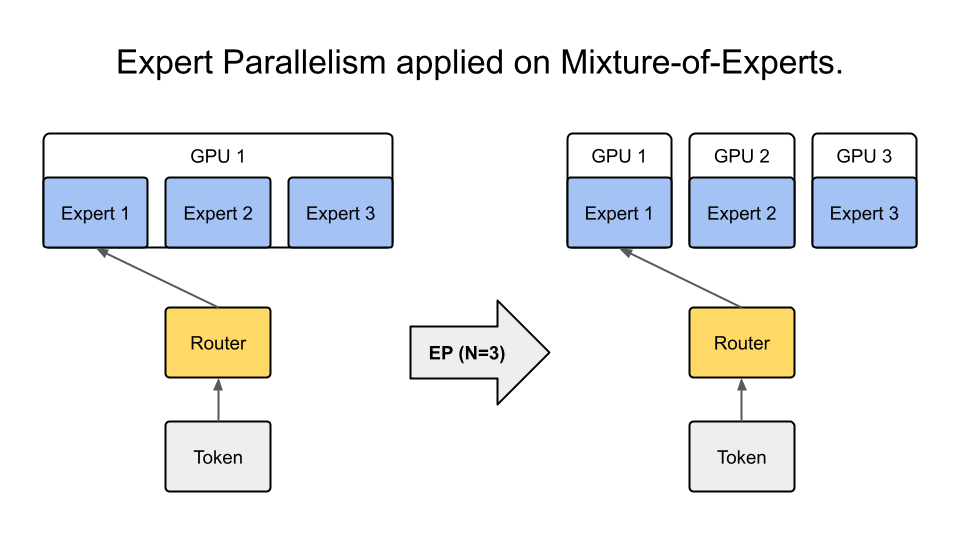
3. 专家并行实现#
专家并行是将不同专家分布到不同设备上的技术，允许模型规模超过单个设备的内存限制。
class ExpertParallelMoE(nn.Module):
"""
专家并行 MoE 实现
将不同专家分布到不同设备上，采用批量处理提高效率
"""
def __init__(self, input_size, output_size, num_experts, expert_hidden_size=64, device_ids=None):
super().__init__()
self.input_size = input_size
self.output_size = output_size
self.num_experts = num_experts
# 设置设备分配（增强：自动适配 CPU/GPU 环境）
if device_ids is None:
if torch.cuda.is_available():
device_ids = list(range(min(num_experts, torch.cuda.device_count())))
else:
device_ids = [torch.device('cpu')]
self.device_ids = device_ids
# 创建专家网络并分配到不同设备
self.experts = nn.ModuleList()
self.expert_devices = [] # 记录每个专家所在的设备
for expert_idx in range(num_experts):
device_id = device_ids[expert_idx % len(device_ids)]
# 确保设备 ID 是有效的设备对象或索引
if isinstance(device_id, str):
device = torch.device(device_id)
else:
device = torch.device(
f"cuda:{device_id}" if device_id != -1 and torch.cuda.is_available() else "cpu"
)
expert = nn.Sequential(
nn.Linear(input_size, expert_hidden_size),
nn.ReLU(),
nn.Linear(expert_hidden_size, output_size)
).to(device)
self.experts.append(expert)
self.expert_devices.append(device)
# 门控网络（在主设备上）
self.main_device = self.expert_devices[0]
self.gate = nn.Linear(input_size, num_experts).to(self.main_device)
def forward(self, x):
"""
专家并行的前向传播（优化版）
批量处理而非单个样本处理，提高效率
"""
# 确保输入在主设备上
x = x.to(self.main_device)
# 计算门控权重
gate_scores = self.gate(x)
gate_probs = F.softmax(gate_scores, dim=-1)
# 选择 top-2 专家
top2_probs, top2_indices = torch.topk(gate_probs, k=2, dim=-1)
top2_probs = top2_probs / top2_probs.sum(dim=-1, keepdim=True)
# 初始化输出张量
final_output = torch.zeros(x.size(0), self.output_size, device=self.main_device)
# 按专家 ID 分组处理，而不是逐个样本处理（核心优化）
for expert_idx in range(self.num_experts):
# 找出所有选择了当前专家的样本和位置
for k in range(2): # 对 top-1 和 top-2 专家分别处理
mask = (top2_indices[:, k] == expert_idx)
if mask.sum() == 0:
continue # 没有样本选择该专家
# 获取对应样本和权重
selected_x = x[mask]
selected_probs = top2_probs[mask, k].unsqueeze(1)
# 将样本发送到专家所在设备
expert_device = self.expert_devices[expert_idx]
x_on_device = selected_x.to(expert_device)
# 计算专家输出
expert_output = self.experts[expert_idx](x_on_device)
# 将结果发送回主设备并加权
final_output[mask] += expert_output.to(self.main_device) * selected_probs
return final_output
# 测试专家并行 MoE
device_ids = [0, 1] if torch.cuda.device_count() >= 2 else ['cpu']
parallel_moe = ExpertParallelMoE(input_size, output_size, num_experts, device_ids=device_ids)
x = torch.randn(batch_size, input_size)
output = parallel_moe(x)
print(f"专家并行 MoE 输出形状: {output.shape}")
print(f"专家设备分配: {[str(dev) for dev in parallel_moe.expert_devices]}")
专家并行实现展示了如何将不同专家分布到不同设备上。这种并行策略的关键优势是允许模型规模超过单个设备的内存限制，同时保持相对较高的计算效率，因为每个输入只使用少数专家。
专家并行 MoE 输出形状: torch.Size([8, 5])
专家设备分配: ['cuda:0', 'cuda:1', 'cuda:0', 'cuda:1']
4. 权重转换与模型缩放#
在大规模模型训练中，权重转换技术用于在不同并行策略间转换模型参数，或者将小模型权重扩展到更大模型。
def expand_model_weights(small_model, large_model, expansion_factor=2):
"""
将小模型权重扩展到大模型
适用于 MoE 模型的专家扩展
"""
small_state_dict = small_model.state_dict()
large_state_dict = large_model.state_dict()
# 复制共享参数
for name, param in small_state_dict.items():
if name in large_state_dict and param.size() == large_state_dict[name].size():
large_state_dict[name] = param
# 扩展专家权重
for name, param in small_state_dict.items():
if 'experts' in name:
# 获取专家索引
expert_idx = int(name.split('.')[1]) # 假设名称格式为 "experts.0.weight"
# 复制到多个专家
for i in range(expansion_factor):
new_expert_idx = expert_idx * expansion_factor + i
new_name = name.replace(f"{expert_idx}", f"{new_expert_idx}")
if new_name in large_state_dict:
large_state_dict[new_name] = param.clone()
# 加载扩展后的权重
large_model.load_state_dict(large_state_dict)
return large_model
# 创建小模型和大模型
small_moe = BasicMoELayer(input_size, output_size, num_experts=2)
large_moe = BasicMoELayer(input_size, output_size, num_experts=4)
print(f"小模型参数数量: {sum(p.numel() for p in small_moe.parameters())}")
print(f"大模型参数数量: {sum(p.numel() for p in large_moe.parameters())}")
# 扩展权重
expanded_moe = expand_model_weights(small_moe, large_moe, expansion_factor=2)
print(f"扩展后模型参数数量: {sum(p.numel() for p in expanded_moe.parameters())}")
# 测试扩展后的模型
x = torch.randn(batch_size, input_size)
output = expanded_moe(x)
print(f"扩展模型输出形状: {output.shape}")
权重转换技术在大规模模型训练中非常重要，它允许我们从小模型开始训练，然后扩展到更大的模型，或者在不同并行配置间转换模型参数。这种方法可以显著减少训练时间和计算资源需求。
5. 简化的大规模训练实践#
下面是一个简化的大规模训练示例，展示了如何使用 MoE 和专家并行进行模型训练。
def train_moe_model():
"""
简化的大规模 MoE 模型训练示例
"""
# 模型参数
input_size = 20
hidden_size = 64
output_size = 10
num_experts = 8
num_classes = 10
# 创建 MoE 模型
moe_model = BasicMoELayer(input_size, hidden_size, num_experts)
classifier = nn.Linear(hidden_size, num_classes)
# 创建优化器
optimizer = torch.optim.Adam(
list(moe_model.parameters()) + list(classifier.parameters()),
lr=0.001
)
criterion = nn.CrossEntropyLoss()
# 模拟训练数据
num_samples = 1000
x_data = torch.randn(num_samples, input_size)
y_data = torch.randint(0, num_classes, (num_samples,))
# 训练循环
num_epochs = 5
batch_size = 32
for epoch in range(num_epochs):
epoch_loss = 0.0
correct = 0
total = 0
for i in range(0, num_samples, batch_size):
# 获取批次数据
x_batch = x_data[i:i+batch_size]
y_batch = y_data[i:i+batch_size]
# 前向传播
moe_output = moe_model(x_batch)
class_output = classifier(moe_output)
# 计算损失
loss = criterion(class_output, y_batch)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 统计
epoch_loss += loss.item()
_, predicted = torch.max(class_output.data, 1)
total += y_batch.size(0)
correct += (predicted == y_batch).sum().item()
accuracy = 100 * correct / total
print(f"Epoch {epoch+1}/{num_epochs}, Loss: {epoch_loss:.4f}, Accuracy: {accuracy:.2f}%")
return moe_model, classifier
# 运行训练
moe_model, classifier = train_moe_model()
这个简化的大规模训练示例展示了如何使用 MoE 模型进行训练。在实际的大规模训练中，还需要考虑数据并行、梯度累积、学习率调度等更复杂的技术。
Epoch 1/5, Loss: 30.8836, Accuracy: 11.30%
Epoch 2/5, Loss: 29.8633, Accuracy: 15.10%
Epoch 3/5, Loss: 29.0344, Accuracy: 17.90%
Epoch 4/5, Loss: 28.2733, Accuracy: 20.50%
Epoch 5/5, Loss: 27.5399, Accuracy: 22.60%
6. 专家负载均衡#
在 MoE 模型中，专家负载均衡是一个重要问题，需要确保所有专家都能得到充分利用。
def calculate_expert_usage(moe_layer, x, top_k=2):
with torch.no_grad():
gate_scores = moe_layer.gate(x)
gate_probs = F.softmax(gate_scores, dim=-1)
# 选择 top-k 专家
topk_probs, topk_indices = torch.topk(gate_probs, k=top_k, dim=-1)
# 计算每个专家的使用次数
expert_usage = torch.zeros(moe_layer.num_experts)
for i in range(x.size(0)):
for j in range(top_k):
expert_idx = topk_indices[i, j].item()
expert_usage[expert_idx] += 1
# 计算使用率（使用次数/总可能使用次数）
total_possible = x.size(0) * top_k
expert_utilization = expert_usage / total_possible
# 计算负载均衡指标（熵值，值越高表示越均衡）
if total_possible > 0:
usage_distribution = expert_usage / total_possible
entropy = -torch.sum(usage_distribution * torch.log(usage_distribution + 1e-10))
else:
entropy = 0.0
return expert_usage, expert_utilization, entropy
# 测试专家使用情况
x_test = torch.randn(100, input_size) # 使用更多测试样本以获得更稳定的统计
expert_usage, expert_utilization, entropy = calculate_expert_usage(moe_model, x_test)
print("专家使用情况:")
for i in range(len(expert_usage)):
print(f"专家 {i}: {expert_usage[i].item()}次 使用，使用率: {expert_utilization[i].item():.2%}")
print(f"负载均衡熵值: {entropy.item():.4f} (值越高表示负载越均衡)")
专家负载均衡是 MoE 模型中的一个关键问题。如果某些专家很少被使用，而其他专家过度使用，会导致模型效率低下。在实际应用中，通常需要添加辅助损失函数来鼓励更均衡的专家使用。
专家使用情况:
专家 0: 32.0 次 使用，使用率: 16.00%
专家 1: 28.0 次 使用，使用率: 14.00%
专家 2: 22.0 次 使用，使用率: 11.00%
专家 3: 26.0 次 使用，使用率: 13.00%
专家 4: 24.0 次 使用，使用率: 12.00%
专家 5: 20.0 次 使用，使用率: 10.00%
专家 6: 20.0 次 使用，使用率: 10.00%
专家 7: 28.0 次 使用，使用率: 14.00%
负载均衡熵值: 2.0672 (值越高表示负载越均衡)
总结与思考#
MoE 技术的核心价值在于能够创建参数量极大但计算效率较高的模型。通过将大型模型分解为多个专家，每个输入只使用少数专家，MoE 可以在保持合理计算成本的同时显著增加模型容量。
专家并行是 MoE 的自然扩展，允许将不同专家分布到不同设备上，从而支持超大规模模型的训练。权重转换技术则提供了模型扩展和并行策略转换的灵活性。