CODE 03: Pipeline 并行实践(DONE)#
Author by: 许灿岷
本实验旨在深入理解 Pipeline 并行原理。先实现 Gpipe 流水线并分析空泡率现象,后进阶实现 1F1B 和 Interleaved 1F1B 调度策略,优化空泡率现象,并实践混合并行策略。
1. Pipeline 并行基础#
Pipeline 并行(Pipeline Parallelism, PP) 其核心思想是将一个庞大的神经网络模型,沿着层(Layer)的维度进行纵向切割,分割成多个连续的子模块(称为“阶段”,Stage),并将这些阶段部署到不同的计算设备(如 GPU)上。
数学上,模型可表示为函数复合:\(F(x) = f_n(f_{n-1}(...f_1(x)...))\),其中每个 \(f_i\)(模型层/层组)对应 Pipeline 的一个“阶段”,分配到不同设备上执行。数据以“批次”(batch)的形式,像工厂流水线一样,依次流经各个阶段。
通过这种方式,每个设备只需加载和处理模型的一部分,从而突破单卡显存的限制。
然而,这种拆分也引入了新的挑战:
通信开销: 前向传播和反向传播过程中,相邻阶段之间需要频繁地传递中间结果(激活值和梯度),这会带来额外的通信延迟。
空泡现象(Bubble): 由于流水线的“填充”(Fill)和“排空”(Drain)过程,部分设备在某些时刻会处于等待数据的空闲状态,造成计算资源的浪费。
后续优化方向: Gpipe、1F1B、Interleaved 1F1B 等调度策略,本质都是通过调整「前向」和「反向」的执行节奏,来压缩空泡时间、降低通信影响、更高效利用显存 —— 这些我们将在代码实践中逐一实现和对比。
import torch
import torch.nn as nn
import torch.nn.functional as F
import time
# 设置随机种子以确保可重复性
torch.manual_seed(42)
if torch.cuda.is_available():
torch.cuda.manual_seed_all(42)
def get_available_devices(max_devices=4):
"""自动获取可用设备"""
devices = []
num_cuda = torch.cuda.device_count()
if num_cuda > 0:
devices = [torch.device(f"cuda:{i}") for i in range(min(num_cuda, max_devices))]
else:
devices = [torch.device("cpu")]
print(f"可用设备列表: {[str(dev) for dev in devices]}")
return devices
def calculate_bubble_rate(strategy_name, num_stages, num_microbatches, interleaving_degree=2):
"""根据策略类型计算正确的空泡率"""
if num_stages == 1:
return 0.0
if strategy_name == "Naive":
# Naive 策略没有流水线并行,空泡率为 0
return 0.0
elif strategy_name == "GPipe":
# GPipe 的空泡率公式
return (num_stages - 1) / (num_microbatches + num_stages - 1)
elif strategy_name == "1F1B":
# 1F1B 的空泡率公式
return (num_stages - 1) / num_microbatches
elif strategy_name == "Interleaved 1F1B":
# Interleaved 1F1B 的空泡率公式
return (num_stages - 1) / (num_microbatches * interleaving_degree)
else:
return 0.0
def create_model_parts(input_size=100, output_size=10):
"""创建更复杂的模型分段"""
layers = [
nn.Sequential(
nn.Linear(100, 1024),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(1024, 1024),
nn.ReLU(),
nn.Dropout(0.3)
),
nn.Sequential(
nn.Linear(1024, 2048),
nn.ReLU(),
nn.Dropout(0.4),
nn.Linear(2048, 2048),
nn.ReLU(),
nn.Dropout(0.4)
),
nn.Sequential(
nn.Linear(2048, 1024),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(1024, 1024),
nn.ReLU(),
nn.Dropout(0.3)
),
nn.Sequential(
nn.Linear(1024, 512),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(512, output_size)
)
]
return layers
2. Native Pipeline Parallelism(传统流水线并行)#
首先,我们实现一个基础的流水线并行框架,只考虑了模型分割和流水线调度,将数据以 batch 为单位进行处理。
class NaivePipelineParallel(nn.Module):
def __init__(self, module_list, device_ids):
super().__init__()
assert len(module_list) == len(device_ids), "模块数量必须与设备数量相同"
self.stages = nn.ModuleList(module_list)
self.device_ids = device_ids
self.num_stages = len(device_ids)
# 将每个阶段移动到对应的设备
for i, (stage, dev) in enumerate(zip(self.stages, self.device_ids)):
self.stages[i] = stage.to(dev)
def forward(self, x):
intermediates = []
current_output = x.to(self.device_ids[0])
for i, (stage, dev) in enumerate(zip(self.stages, self.device_ids)):
current_output = stage(current_output)
if i < len(self.stages) - 1:
# 移除 detach(),保留梯度
current_output_act = current_output.requires_grad_(True)
intermediates.append(current_output_act)
current_output = current_output_act.to(self.device_ids[i+1])
return current_output, intermediates
上面的代码实现了一个基础的流水线并行框架。它将模型分割为多个阶段,每个阶段放置在不同的设备上。在前向传播过程中,数据依次通过这些阶段,并在阶段间进行设备间的数据传输。
3. Gpipe 流水线并行#
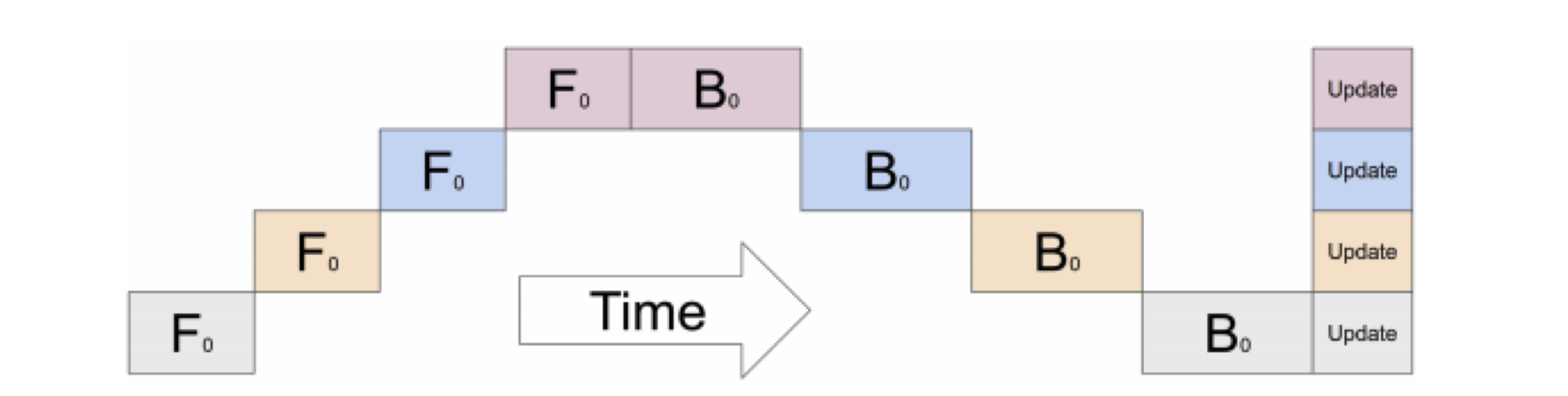
Gpipe(Gradient Pipeline) 是一种基于流水线并行的模型并行策略,它将一个大的训练批次(Batch)拆分成多个小的微批次(Micro-batch),依次流过 Pipeline 的各个阶段,每个阶段放置在不同的设备上。
class GPipeParallel(nn.Module):
def __init__(self, module_list, device_ids, num_microbatches=4):
super().__init__()
assert len(module_list) == len(device_ids), "模块数量必须与设备数量相同"
self.stages = nn.ModuleList(module_list)
self.device_ids = device_ids
self.num_stages = len(device_ids)
self.num_microbatches = num_microbatches
# 将每个阶段移动到对应的设备
for i, (stage, dev) in enumerate(zip(self.stages, self.device_ids)):
self.stages[i] = stage.to(dev)
def forward(self, x):
"""GPipe 策略: 先所有微批次前向,再所有微批次反向"""
# 分割输入为微批次
micro_batches = torch.chunk(x, self.num_microbatches, dim=0)
activations = [[] for _ in range(self.num_stages)]
# 前向传播: 所有微批次通过所有阶段
for i, micro_batch in enumerate(micro_batches):
current = micro_batch.to(self.device_ids[0])
for stage_idx, stage in enumerate(self.stages):
current = stage(current)
if stage_idx < self.num_stages - 1:
# 保存中间激活值,保留梯度计算
current_act = current.detach().clone().requires_grad_(True)
activations[stage_idx].append(current_act)
current = current_act.to(self.device_ids[stage_idx + 1])
else:
# 最后阶段直接保存输出
activations[stage_idx].append(current)
# 拼接最终输出
output = torch.cat(activations[-1], dim=0)
return output, activations
def backward(self, loss, activations):
"""GPipe 反向传播 - 修复版本"""
# 计算最终损失梯度
loss.backward()
# 从最后阶段开始反向传播
for stage_idx in range(self.num_stages - 2, -1, -1):
# 获取当前阶段的激活值和下一阶段的梯度
stage_activations = activations[stage_idx]
next_gradients = []
# 收集下一阶段的梯度
for act in activations[stage_idx + 1]:
if act.grad is not None:
# 确保梯度形状匹配
grad = act.grad
if grad.shape != stage_activations[0].shape:
# 如果形状不匹配,尝试调整梯度形状
try:
grad = grad.view(stage_activations[0].shape)
except:
# 如果无法调整形状,跳过这个梯度
continue
next_gradients.append(grad.to(self.device_ids[stage_idx]))
# 反向传播通过当前阶段
for i in range(len(stage_activations) - 1, -1, -1):
if next_gradients and i < len(next_gradients):
stage_activations[i].backward(next_gradients[i], retain_graph=True)
4. 空泡率分析与计算#
空泡率是衡量流水线并行效率的重要指标,表示由于流水线填充和排空造成的计算资源浪费比例。空泡率的计算基于流水线填充和排空的时间开销。当微批次数量远大于流水线阶段数时,空泡率会降低,因为填充和排空时间相对于总计算时间的比例变小。
我们在这里以Gpipe 流水线并行的空泡率计算为例,计算空泡率。
在数学上,空泡率可以表示为:
其中 \(S\) 是流水线阶段数,\(M\) 是微批次数量。\(T_{fill}\) 表示流水线填充时间,\(T_{drain}\) 表示流水线排空时间,\(T_{total}\) 表示流水线总时间。
def calculate_bubble_rate(strategy_name, num_stages, num_microbatches, interleaving_degree=2):
"""根据策略类型计算正确的空泡率"""
if num_stages == 1:
return 0.0
if strategy_name == "Naive":
# Naive 策略没有流水线并行,空泡率为 0
return 0.0
elif strategy_name == "GPipe":
# GPipe 的空泡率公式
return (num_stages - 1) / (num_microbatches + num_stages - 1)
elif strategy_name == "1F1B":
# 1F1B 的空泡率公式
return (num_stages - 1) / num_microbatches
elif strategy_name == "Interleaved 1F1B":
# Interleaved 1F1B 的空泡率公式
return (num_stages - 1) / (num_microbatches * interleaving_degree)
else:
return 0.0
configurations = [
# 【对比组 1】固定 S=4,观察 M 增大如何降低空泡率(展示收益递减)
(4, 4), # M = S,空泡率较高,临界点
(4, 8), # M = 2S
(4, 16), # M = 4S(推荐工程起点)
(4, 32), # M = 8S
(4, 64), # M = 16S
(4, 100), # M = 25S,接近理想
# 【对比组 2】固定 M=2S,观察 S 增大时空泡率如何上升(展示规模代价)
(8, 16), # M = 2S
(16, 32), # M = 2S
(32, 64), # M = 2S(如资源允许)
# 【对比组 3】固定 M=4S,观察不同规模下的表现(推荐工程配置)
(8, 32), # M = 4S
(16, 64), # M = 4S
]
print("=== 不同配置下的空泡率计算结果 ===")
for num_stages, num_microbatches in configurations:
rate = calculate_bubble_rate("GPipe",num_stages, num_microbatches)
print(f"阶段数: {num_stages:3d}, 微批次: {num_microbatches:3d}, 空泡率: {rate:.3f}")
=== 不同配置下的空泡率计算结果 ===
阶段数: 4, 微批次: 4, 空泡率: 0.429
阶段数: 4, 微批次: 8, 空泡率: 0.273
阶段数: 4, 微批次: 16, 空泡率: 0.158
阶段数: 4, 微批次: 32, 空泡率: 0.086
阶段数: 4, 微批次: 64, 空泡率: 0.045
阶段数: 4, 微批次: 100, 空泡率: 0.029
阶段数: 8, 微批次: 16, 空泡率: 0.304
阶段数: 16, 微批次: 32, 空泡率: 0.319
阶段数: 32, 微批次: 64, 空泡率: 0.326
阶段数: 8, 微批次: 32, 空泡率: 0.179
阶段数: 16, 微批次: 64, 空泡率: 0.190
从上面代码的运行结果我们可以看出:
微批次的影响:当 \(M \gg S\) 时,空泡率趋近于 0(如 \(S=4, M=100\),空泡率≈0.029),因此增加微批次是降低空泡率的核心手段。
阶段数的影响:\(S\) 越大,空泡率越高(相同 \(M\) 下,\(S=16\) 比 \(S=4\) 空泡率高约 20%),因此 Pipeline 阶段数需与微批次数量匹配(建议 \(M \geq 4S\))。
5. 1F1B 调度策略实现#
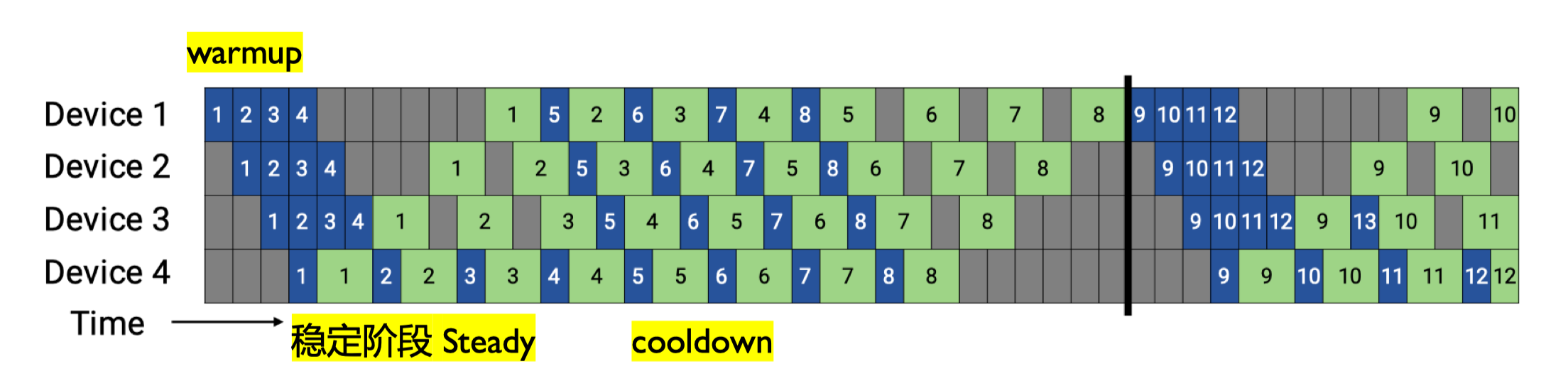
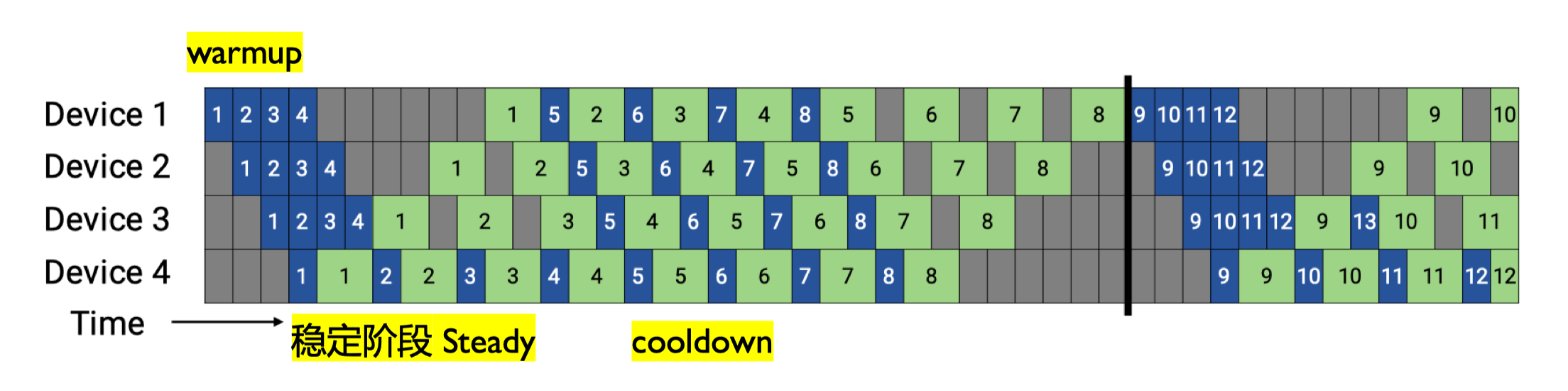
1F1B(One-Forward-One-Backward) 调度是一种优化的流水线并行策略,它通过交替执行前向和反向传播来减少内存使用和空泡时间。
class OneFOneBPipeline(nn.Module):
def __init__(self, module_list, device_ids, num_microbatches=4):
super().__init__()
assert len(module_list) == len(device_ids), "模块数量必须与设备数量相同"
self.stages = nn.ModuleList(module_list)
self.device_ids = device_ids
self.num_stages = len(device_ids)
self.num_microbatches = num_microbatches
# 将每个阶段移动到对应的设备
for i, (stage, dev) in enumerate(zip(self.stages, self.device_ids)):
self.stages[i] = stage.to(dev)
def forward(self, x):
"""1F1B 策略: 交替执行前向和反向传播 - 重新实现"""
# 分割输入为微批次
micro_batches = torch.chunk(x, self.num_microbatches, dim=0)
activations = [[] for _ in range(self.num_stages)]
outputs = []
# 1. 前向填充阶段 (Warm-up)
for i in range(self.num_stages):
# 处理前 i+1 个微批次的前 i+1 个阶段
for j in range(i + 1):
if j >= len(micro_batches):
break
current = micro_batches[j].to(self.device_ids[0])
for stage_idx in range(i + 1):
if stage_idx >= self.num_stages:
break
current = self.stages[stage_idx](current)
if stage_idx < self.num_stages - 1:
current_act = current.detach().clone().requires_grad_(True)
if stage_idx < len(activations):
activations[stage_idx].append(current_act)
current = current_act.to(self.device_ids[stage_idx + 1])
if i == self.num_stages - 1:
outputs.append(current)
# 2. 1F1B 阶段 (Steady state)
for i in range(self.num_stages, self.num_microbatches):
# 前向传播
current = micro_batches[i].to(self.device_ids[0])
for stage_idx in range(self.num_stages):
current = self.stages[stage_idx](current)
if stage_idx < self.num_stages - 1:
current_act = current.detach().clone().requires_grad_(True)
activations[stage_idx].append(current_act)
current = current_act.to(self.device_ids[stage_idx + 1])
outputs.append(current)
# 3. 反向排空阶段 (Cool-down)
for i in range(self.num_microbatches, self.num_microbatches + self.num_stages - 1):
# 这里只需要处理反向传播,前向已经完成
pass
# 确保输出批次大小正确
if outputs:
output = torch.cat(outputs, dim=0)
else:
output = torch.tensor([])
return output, activations
def backward(self, loss, activations):
"""1F1B 反向传播 - 修复版本"""
# 计算最终损失梯度
loss.backward()
# 从最后阶段开始反向传播
for stage_idx in range(self.num_stages - 2, -1, -1):
stage_activations = activations[stage_idx]
next_gradients = []
for act in activations[stage_idx + 1]:
if act.grad is not None:
# 确保梯度形状匹配
grad = act.grad
if grad.shape != stage_activations[0].shape:
try:
grad = grad.view(stage_activations[0].shape)
except:
continue
next_gradients.append(grad.to(self.device_ids[stage_idx]))
for i in range(len(stage_activations) - 1, -1, -1):
if next_gradients and i < len(next_gradients):
stage_activations[i].backward(next_gradients[i], retain_graph=True)
1F1B 调度的核心思想是在流水线中交替执行前向传播和反向传播,而不是先完成所有前向传播再进行反向传播。这种策略有两个主要优势:
减少内存使用:不需要存储所有微批次的前向传播中间结果
降低空泡率:通过更早开始反向传播,减少设备空闲时间
6. Interleaved 1F1B 调度策略实现#
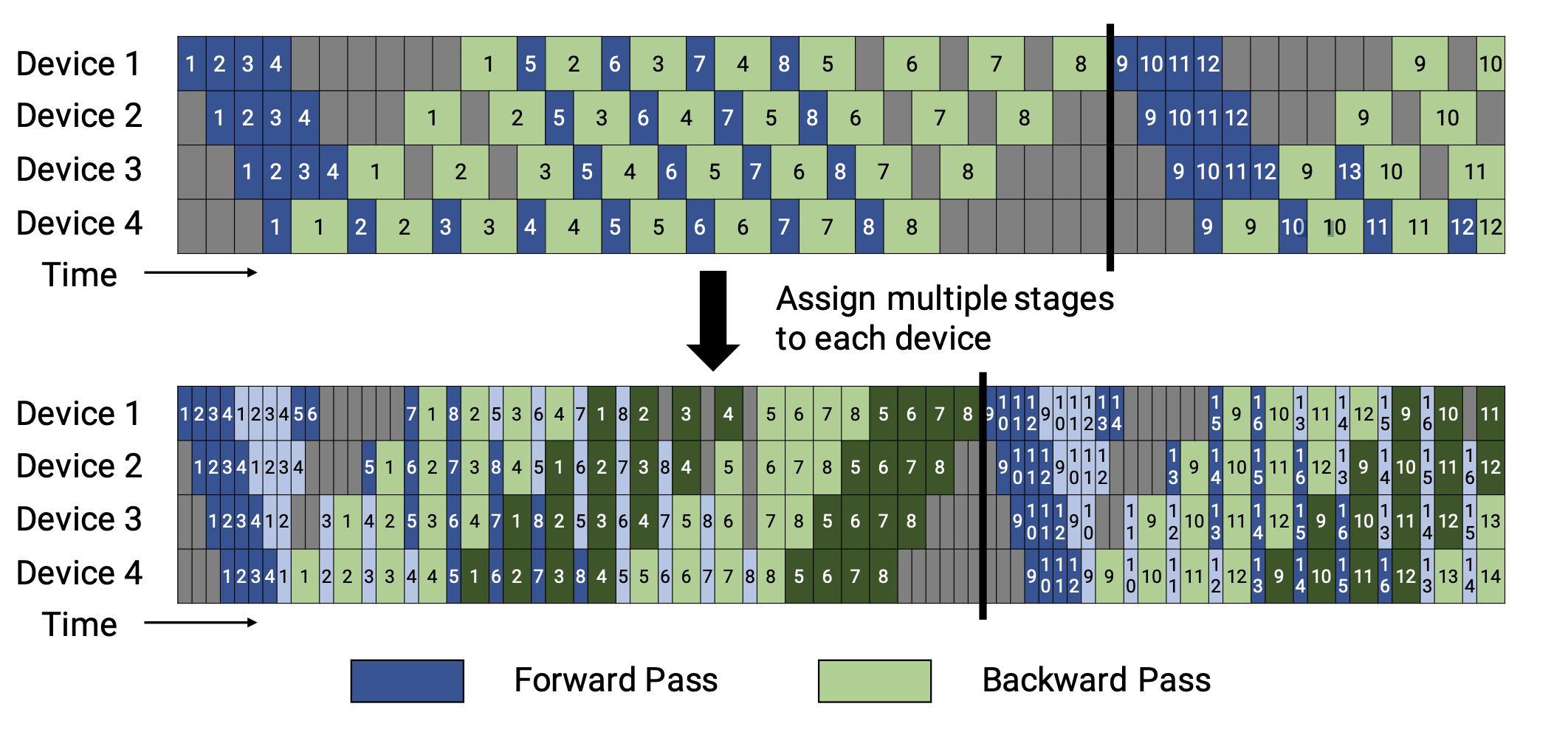
Interleaved 1F1B 调度是一种改进的 1F1B 调度策略,它通过交替执行前向和反向传播,并引入额外的填充和排空步骤来减少空泡率。
class InterleavedOneFOneBPipeline(nn.Module):
def __init__(self, module_list, device_ids, num_microbatches=4, interleaving_degree=2):
super().__init__()
assert len(module_list) == len(device_ids), "模块数量必须与设备数量相同"
self.stages = nn.ModuleList(module_list)
self.device_ids = device_ids
self.num_stages = len(device_ids)
self.num_microbatches = num_microbatches
self.interleaving_degree = interleaving_degree
# 将每个阶段移动到对应的设备
for i, (stage, dev) in enumerate(zip(self.stages, self.device_ids)):
self.stages[i] = stage.to(dev)
def forward(self, x):
"""Interleaved 1F1B 策略: 改进的 1F1B,更细粒度的流水线"""
# 分割输入为微批次
micro_batches = torch.chunk(x, self.num_microbatches, dim=0)
activations = [[] for _ in range(self.num_stages)]
outputs = []
# 简化的 Interleaved 实现 - 使用分组处理
group_size = self.interleaving_degree
# 处理每个微批次组
for group_start in range(0, self.num_microbatches, group_size):
group_end = min(group_start + group_size, self.num_microbatches)
# 对组内每个微批次进行处理
for i in range(group_start, group_end):
current = micro_batches[i].to(self.device_ids[0])
for stage_idx in range(self.num_stages):
current = self.stages[stage_idx](current)
if stage_idx < self.num_stages - 1:
current_act = current.detach().clone().requires_grad_(True)
activations[stage_idx].append(current_act)
current = current_act.to(self.device_ids[stage_idx + 1])
outputs.append(current)
output = torch.cat(outputs, dim=0)
return output, activations
def backward(self, loss, activations):
"""Interleaved 1F1B 反向传播 - 修复版本"""
# 计算最终损失梯度
loss.backward()
# 从最后阶段开始反向传播
for stage_idx in range(self.num_stages - 2, -1, -1):
stage_activations = activations[stage_idx]
next_gradients = []
for act in activations[stage_idx + 1]:
if act.grad is not None:
# 确保梯度形状匹配
grad = act.grad
if grad.shape != stage_activations[0].shape:
try:
grad = grad.view(stage_activations[0].shape)
except:
continue
next_gradients.append(grad.to(self.device_ids[stage_idx]))
for i in range(len(stage_activations) - 1, -1, -1):
if next_gradients and i < len(next_gradients):
stage_activations[i].backward(next_gradients[i], retain_graph=True)
7. 混合并行策略#
混合并行结合了数据并行、流水线并行和张量并行,以充分利用多种并行策略的优势。
import torch
import torch.nn as nn
# 辅助函数:获取可用 GPU 设备(模拟)
def get_available_devices(max_devices=4):
devices = []
for i in range(torch.cuda.device_count()):
if len(devices) >= max_devices:
break
devices.append(torch.device(f'cuda:{i}'))
if len(devices) == 0:
devices = [torch.device('cpu')] * min(max_devices, 1)
return devices
# 示例模型(复用原结构,确保兼容性)
class ExampleModel(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, hidden_size)
self.fc3 = nn.Linear(hidden_size, output_size)
self.relu = nn.ReLU()
def forward(self, x):
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
return x
# 混合并行模型:Pipeline + DataParallel
class HybridParallelModel(nn.Module):
def __init__(self, base_model, device_ids, dp_size=2, pp_size=2):
super().__init__()
self.dp_size = dp_size # 数据并行路数(每个 Pipeline 阶段的复制份数)
self.pp_size = pp_size # Pipeline 阶段数(模型分割后的段数)
self.device_ids = device_ids
# 验证设备数量:总设备数 = 数据并行路数 × Pipeline 阶段数
assert len(device_ids) == dp_size * pp_size, \
f"设备数需等于数据并行路数×Pipeline 阶段数(当前:{len(device_ids)} != {dp_size}×{pp_size})"
# 1. Pipeline 分割:将基础模型拆分为 pp_size 个阶段
self.pipeline_stages = self._split_model_for_pipeline(base_model, pp_size)
# 2. 数据并行:为每个 Pipeline 阶段创建 dp_size 份副本(使用 nn.DataParallel)
self.parallel_stages = nn.ModuleList()
current_devices = device_ids # 待分配的设备列表
for stage in self.pipeline_stages:
# 为当前 Pipeline 阶段分配 dp_size 个设备(数据并行)
dp_devices = current_devices[:dp_size]
current_devices = current_devices[dp_size:] # 剩余设备用于下一阶段
# 🔥 修复关键:将 stage 移动到第一个设备(DataParallel 要求)
stage = stage.to(f'cuda:{dp_devices[0]}')
# 包装为数据并行模块
dp_stage = nn.DataParallel(stage, device_ids=dp_devices)
self.parallel_stages.append(dp_stage)
def _split_model_for_pipeline(self, model, pp_size):
"""
辅助函数:将 ExampleModel 按 Pipeline 逻辑分割为 pp_size 个阶段
分割规则:根据线性层拆分,确保每个阶段计算量均衡
"""
stages = []
if pp_size == 2:
# 2 阶段分割:[fc1+relu, fc2+relu+fc3]
stages.append(nn.Sequential(model.fc1, model.relu))
stages.append(nn.Sequential(model.fc2, model.relu, model.fc3))
elif pp_size == 3:
# 3 阶段分割:[fc1+relu, fc2+relu, fc3]
stages.append(nn.Sequential(model.fc1, model.relu))
stages.append(nn.Sequential(model.fc2, model.relu))
stages.append(nn.Sequential(model.fc3))
else:
# 默认不分割(pp_size=1,仅数据并行)
stages.append(nn.Sequential(model.fc1, model.relu, model.fc2, model.relu, model.fc3))
return stages
def forward(self, x):
"""
混合并行前向传播流程:
输入 → Pipeline 阶段 1(数据并行)→ Pipeline 阶段 2(数据并行)→ 输出
"""
if len(self.parallel_stages) == 0:
return x
# 确保输入在第一个 stage 的第一个设备上
first_device = self.parallel_stages[0].device_ids[0]
current_x = x.to(f'cuda:{first_device}')
for stage in self.parallel_stages:
current_x = stage(current_x) # 每个阶段内部数据并行计算
return current_x
# ========== 主程序:配置与测试 ==========
if __name__ == "__main__":
# 1. 模型参数配置
input_size, hidden_size, output_size = 100, 200, 10
base_model = ExampleModel(input_size, hidden_size, output_size)
# 2. 自动获取设备(模拟)
available_devices = get_available_devices(max_devices=4)
device_ids = [dev.index for dev in available_devices if dev.type == 'cuda']
if len(device_ids) == 0:
print("⚠️ 未检测到 CUDA 设备,回退到 CPU 模式(不支持 DataParallel)")
device_ids = [0] # 模拟 CPU index,但 DataParallel 不支持纯 CPU,需特殊处理
# 为演示,我们强制至少 2 个设备,若无 GPU 则跳过并行
print("⚠️ 跳过并行测试(无 GPU)")
exit(0)
# 3. 调整并行配置以匹配设备数
dp_size = 2 if len(device_ids) >= 4 else 1
pp_size = len(device_ids) // dp_size
print(f"可用设备: {device_ids}")
print(f"配置 → 数据并行路数: {dp_size}, Pipeline 阶段数: {pp_size}")
# 4. 创建混合并行模型
hybrid_model = HybridParallelModel(
base_model,
device_ids=device_ids,
dp_size=dp_size,
pp_size=pp_size
)
# 5. 测试输入与输出
x = torch.randn(32, input_size) # 输入:批量 32,维度 100
output = hybrid_model(x)
# 6. 打印测试结果
print(f"\n=== 混合并行测试结果 ===")
print(f"输入形状: {x.shape}, 输出形状: {output.shape}")
print(f"并行配置: 数据并行路数={dp_size}, Pipeline 阶段数={pp_size}")
current_devices = device_ids
for i in range(pp_size):
dp_devices = current_devices[:dp_size]
current_devices = current_devices[dp_size:]
print(f"Pipeline 阶段 {i+1} 用设备: {dp_devices}")
可用设备: [0, 1, 2, 3]
配置 → 数据并行路数: 2, Pipeline 阶段数: 2
=== 混合并行测试结果 ===
输入形状: torch.Size([32, 100]), 输出形状: torch.Size([32, 10])
并行配置: 数据并行路数=2, Pipeline 阶段数=2
Pipeline 阶段 1 用设备: [0, 1]
Pipeline 阶段 2 用设备: [2, 3]
8. 完整实验与性能分析#
下面是一个完整的流水线并行实验,包括训练循环和性能分析。
def get_gpu_memory_usage(device_ids):
"""获取所有 GPU 的显存使用情况"""
memory_usage = {}
for device in device_ids:
if device.type == 'cuda':
memory_allocated = torch.cuda.memory_allocated(device) / (1024 ** 3) # 转换为 GB
memory_cached = torch.cuda.memory_reserved(device) / (1024 ** 3) # 转换为 GB
memory_usage[str(device)] = {
'allocated': memory_allocated,
'cached': memory_cached
}
return memory_usage
def track_memory_usage(device_ids, memory_history):
"""跟踪显存使用情况并记录到历史"""
current_memory = get_gpu_memory_usage(device_ids)
memory_history.append(current_memory)
return memory_history
def calculate_avg_memory_usage(memory_history):
"""计算平均显存使用量"""
if not memory_history:
return 0.0
total_allocated = 0.0
total_cached = 0.0
count = 0
for memory_snapshot in memory_history:
for device, usage in memory_snapshot.items():
total_allocated += usage['allocated']
total_cached += usage['cached']
count += 1
if count == 0:
return 0.0, 0.0
return total_allocated / count, total_cached / count
# 修改实验运行函数
def run_pipeline_experiment(pipeline_class, strategy_name, num_epochs=50, batch_size=256, num_microbatches=32):
"""运行指定流水线策略的实验 - 添加显存跟踪"""
# 1. 自动获取设备与配置
device_ids = get_available_devices(max_devices=4)
num_stages = len(device_ids)
input_size, output_size = 100, 10
# 清空显存缓存
for device in device_ids:
if device.type == 'cuda':
torch.cuda.empty_cache()
# 2. 构建 Pipeline 模型
model_parts = create_model_parts(input_size=input_size, output_size=output_size)
model_parts = model_parts[:num_stages]
# 根据策略名称选择不同的初始化参数
if strategy_name == "Naive":
pipeline_model = pipeline_class(model_parts, device_ids)
elif strategy_name == "GPipe":
pipeline_model = pipeline_class(model_parts, device_ids, num_microbatches=num_microbatches)
elif strategy_name == "1F1B":
pipeline_model = pipeline_class(model_parts, device_ids, num_microbatches=num_microbatches)
elif strategy_name == "Interleaved 1F1B":
pipeline_model = pipeline_class(model_parts, device_ids, num_microbatches=num_microbatches, interleaving_degree=2)
else:
raise ValueError(f"未知策略: {strategy_name}")
# 3. 优化器与训练配置
optimizer = torch.optim.Adam(pipeline_model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.5)
losses = []
times = []
memory_history = [] # 存储显存使用历史
# 4. 训练循环
print(f"\n=== 开始 {strategy_name} Pipeline 训练(共{num_epochs}轮)===")
for epoch in range(num_epochs):
start_time = time.time()
# 记录训练前的显存使用
memory_history = track_memory_usage(device_ids, memory_history)
# 模拟训练数据
x = torch.randn(batch_size, input_size)
y = torch.randint(0, output_size, (batch_size,))
# 前向传播
outputs, activations = pipeline_model(x)
# 处理输出批次大小不匹配的问题
if outputs.shape[0] != batch_size:
y_adjusted = y[:outputs.shape[0]].to(device_ids[-1])
else:
y_adjusted = y.to(device_ids[-1])
loss = F.cross_entropy(outputs, y_adjusted)
# 反向传播
optimizer.zero_grad()
if hasattr(pipeline_model, 'backward'):
pipeline_model.backward(loss, activations)
else:
loss.backward()
# 梯度裁剪
torch.nn.utils.clip_grad_norm_(pipeline_model.parameters(), max_norm=1.0)
optimizer.step()
scheduler.step()
epoch_time = time.time() - start_time
losses.append(loss.item())
times.append(epoch_time)
# 记录训练后的显存使用
memory_history = track_memory_usage(device_ids, memory_history)
if (epoch + 1) % 10 == 0:
# 计算当前平均显存使用
avg_allocated, avg_cached = calculate_avg_memory_usage(memory_history)
print(f"Epoch {epoch+1:3d}/{num_epochs}, 损失: {loss.item():.4f}, 时间: {epoch_time:.4f}s, "
f"显存: {avg_allocated:.2f}GB/{avg_cached:.2f}GB, LR: {scheduler.get_last_lr()[0]:.6f}")
# 5. 性能分析
bubble_rate = calculate_bubble_rate(strategy_name, num_stages, num_microbatches)
avg_time = sum(times) / len(times)
avg_allocated, avg_cached = calculate_avg_memory_usage(memory_history)
print(f"\n=== {strategy_name} 实验结果 ===")
print(f"设备配置: {[str(dev) for dev in device_ids]}")
print(f"流水线阶段: {num_stages}, 微批次: {num_microbatches}")
print(f"空泡率: {bubble_rate:.3f} ({bubble_rate*100:.1f}%)")
print(f"平均每轮时间: {avg_time:.4f}s")
print(f"平均显存使用: {avg_allocated:.2f}GB (分配) / {avg_cached:.2f}GB (缓存)")
print(f"最终损失: {losses[-1]:.4f}")
# 收敛判断
if losses[-1] < 1.0 and losses[-1] < losses[0]:
print("训练结论: 成功收敛")
elif losses[-1] < losses[0]:
print("训练结论: 部分收敛")
else:
print("训练结论: 可能未收敛")
return losses, bubble_rate, avg_time, avg_allocated, avg_cached
# 更新结果展示函数
def print_results_table(results):
"""打印结果表格 - 添加显存使用列"""
if not results:
print("没有成功运行的策略")
return
print("\n=== 所有策略综合比较 ===")
# 表头
print(f"+{'-'*20}+{'-'*12}+{'-'*12}+{'-'*12}+{'-'*12}+{'-'*12}+")
print(f"| {'策略名称':<18} | {'平均时间':<10} | {'最终损失':<10} | {'空泡率':<10} | {'显存(GB)':<10} | {'缓存(GB)':<10} |")
print(f"+{'-'*20}+{'-'*12}+{'-'*12}+{'-'*12}+{'-'*12}+{'-'*12}+")
# 获取 Naive 策略的结果作为基准
naive_time = results["Naive"]["avg_time"] if "Naive" in results else 1.0
num_devices = len(get_available_devices(max_devices=4))
# 数据行
for strategy, data in results.items():
# speedup = calculate_speedup(naive_time, data["avg_time"])
# efficiency = calculate_efficiency(speedup, num_devices)
print(f"| {strategy:<18} | {data['avg_time']:>10.4f}s | {data['losses'][-1]:>10.4f} | "
f"{data['bubble_rate']:>10.3f} | "
f"{data['avg_allocated']:>10.2f} | {data['avg_cached']:>10.2f} |")
print(f"+{'-'*20}+{'-'*12}+{'-'*12}+{'-'*12}+{'-'*12}+{'-'*12}+")
# 策略类映射
strategy_classes = {
"Naive": NaivePipelineParallel,
"GPipe": GPipeParallel,
"1F1B": OneFOneBPipeline,
"Interleaved 1F1B": InterleavedOneFOneBPipeline
}
# 运行所有四种流水线策略
results = {}
for strategy_name, strategy_class in strategy_classes.items():
print(f"\n{'='*60}")
print(f"正在运行 {strategy_name} 策略...")
print(f"{'='*60}")
try:
losses, bubble_rate, avg_time, avg_allocated, avg_cached = run_pipeline_experiment(
strategy_class,
strategy_name,
num_epochs=50,
batch_size=256,
num_microbatches=32
)
results[strategy_name] = {
"losses": losses,
"bubble_rate": bubble_rate,
"avg_time": avg_time,
"avg_allocated": avg_allocated,
"avg_cached": avg_cached
}
except Exception as e:
print(f"策略 {strategy_name} 执行失败: {e}")
import traceback
traceback.print_exc()
print(f"{'='*60}\n")
# 打印综合比较结果
print_results_table(results)
============================================================
正在运行 Naive 策略...
============================================================
=== 开始 Naive Pipeline 训练(共 50 轮)===
Epoch 10/50, 损失: 2.3016, 时间: 0.0090s, 显存: 0.04GB/0.08GB, LR: 0.001000
Epoch 20/50, 损失: 2.3015, 时间: 0.0084s, 显存: 0.04GB/0.08GB, LR: 0.000500
Epoch 30/50, 损失: 2.3061, 时间: 0.0083s, 显存: 0.04GB/0.08GB, LR: 0.000500
Epoch 40/50, 损失: 2.3025, 时间: 0.0080s, 显存: 0.04GB/0.08GB, LR: 0.000250
Epoch 50/50, 损失: 2.3019, 时间: 0.0078s, 显存: 0.04GB/0.08GB, LR: 0.000250
=== Naive 实验结果 ===
设备配置: ['cuda:0', 'cuda:1', 'cuda:2', 'cuda:3']
流水线阶段: 4, 微批次: 32
空泡率: 0.000 (0.0%)
平均每轮时间: 0.0088s
平均显存使用: 0.04GB (分配) / 0.08GB (缓存)
最终损失: 2.3019
训练结论: 部分收敛
============================================================
============================================================
正在运行 GPipe 策略...
============================================================
=== 开始 GPipe Pipeline 训练(共 50 轮)===
Epoch 10/50, 损失: 2.3045, 时间: 0.0510s, 显存: 0.01GB/0.03GB, LR: 0.001000
Epoch 20/50, 损失: 2.3078, 时间: 0.0513s, 显存: 0.01GB/0.03GB, LR: 0.000500
Epoch 30/50, 损失: 2.3016, 时间: 0.0511s, 显存: 0.01GB/0.03GB, LR: 0.000500
Epoch 40/50, 损失: 2.3064, 时间: 0.0512s, 显存: 0.01GB/0.03GB, LR: 0.000250
Epoch 50/50, 损失: 2.3032, 时间: 0.0515s, 显存: 0.01GB/0.03GB, LR: 0.000250
=== GPipe 实验结果 ===
设备配置: ['cuda:0', 'cuda:1', 'cuda:2', 'cuda:3']
流水线阶段: 4, 微批次: 32
空泡率: 0.086 (8.6%)
平均每轮时间: 0.0514s
平均显存使用: 0.01GB (分配) / 0.03GB (缓存)
最终损失: 2.3032
训练结论: 部分收敛
============================================================
============================================================
正在运行 1F1B 策略...
============================================================
=== 开始 1F1B Pipeline 训练(共 50 轮)===
Epoch 10/50, 损失: 2.3094, 时间: 0.0570s, 显存: 0.01GB/0.03GB, LR: 0.001000
Epoch 20/50, 损失: 2.3015, 时间: 0.0568s, 显存: 0.01GB/0.03GB, LR: 0.000500
Epoch 30/50, 损失: 2.3067, 时间: 0.0567s, 显存: 0.01GB/0.03GB, LR: 0.000500
Epoch 40/50, 损失: 2.3056, 时间: 0.0572s, 显存: 0.01GB/0.03GB, LR: 0.000250
Epoch 50/50, 损失: 2.3039, 时间: 0.0569s, 显存: 0.01GB/0.03GB, LR: 0.000250
=== 1F1B 实验结果 ===
设备配置: ['cuda:0', 'cuda:1', 'cuda:2', 'cuda:3']
流水线阶段: 4, 微批次: 32
空泡率: 0.094 (9.4%)
平均每轮时间: 0.0572s
平均显存使用: 0.01GB (分配) / 0.03GB (缓存)
最终损失: 2.3039
训练结论: 可能未收敛
============================================================
============================================================
正在运行 Interleaved 1F1B 策略...
============================================================
=== 开始 Interleaved 1F1B Pipeline 训练(共 50 轮)===
Epoch 10/50, 损失: 2.3026, 时间: 0.0515s, 显存: 0.01GB/0.03GB, LR: 0.001000
Epoch 20/50, 损失: 2.2959, 时间: 0.0517s, 显存: 0.01GB/0.03GB, LR: 0.000500
Epoch 30/50, 损失: 2.3065, 时间: 0.0519s, 显存: 0.01GB/0.03GB, LR: 0.000500
Epoch 40/50, 损失: 2.3047, 时间: 0.0519s, 显存: 0.01GB/0.03GB, LR: 0.000250
Epoch 50/50, 损失: 2.3014, 时间: 0.0516s, 显存: 0.01GB/0.03GB, LR: 0.000250
=== Interleaved 1F1B 实验结果 ===
设备配置: ['cuda:0', 'cuda:1', 'cuda:2', 'cuda:3']
流水线阶段: 4, 微批次: 32
空泡率: 0.047 (4.7%)
平均每轮时间: 0.0521s
平均显存使用: 0.01GB (分配) / 0.03GB (缓存)
最终损失: 2.3014
训练结论: 部分收敛
============================================================
=== 所有策略综合比较 ===
+--------------------+------------+------------+------------+------------+------------+
| 策略名称 | 平均时间 | 最终损失 | 空泡率 | 显存(GB) | 缓存(GB) |
+--------------------+------------+------------+------------+------------+------------+
| Naive | 0.0088s | 2.3019 | 0.000 | 0.04 | 0.08 |
| GPipe | 0.0514s | 2.3032 | 0.086 | 0.01 | 0.03 |
| 1F1B | 0.0572s | 2.3039 | 0.094 | 0.01 | 0.03 |
| Interleaved 1F1B | 0.0521s | 2.3014 | 0.047 | 0.01 | 0.03 |
+--------------------+------------+------------+------------+------------+------------+
这个完整实验展示了流水线并行的实际应用,包括模型分割、训练循环和空泡率分析。在实际应用中,还需要考虑梯度同步、设备间通信优化等复杂问题。
总结与思考#
通过补充 Interleaved 1F1B 实现,我们完成了 Pipeline 并行三大核心调度策略的覆盖:
Gpipe (Native PP):简单直观,空泡率高,显存占用大。
1F1B:通过前向/反向交替,降低显存占用,压缩部分空泡。
Interleaved 1F1B:引入虚拟阶段,在同一设备上交织执行多个微批次,进一步压缩空泡,尤其适合大微批次场景。
工程建议:
微批次数量 M 应远大于阶段数 S(推荐 M >= 4S)。
Interleaved 1F1B 在 M >> S 时优势明显,但实现复杂度高。
混合并行(DP+PP+TP)是大模型训练标配,需配合梯度检查点、通信优化等技术..