CODE 02: MOE 参数量和计算量

CODE 02: MOE 参数量和计算量#

在深度学习领域，模型规模的增长往往带来性能的提升，但同时也伴随着计算成本的急剧增加。混合专家模型（Mixture of Experts, MOE）作为一种稀疏激活的模型结构，通过仅激活部分"专家"网络来在保持参数量的同时控制计算量，成为了大模型领域的重要技术突破。

下面将通过简单的代码实现和理论分析，帮助初学者理解MOE模型的参数量和计算量评估方法，以及在训练和推理过程中的差异。

1. MOE基本原理#

MOE模型的核心思想是将一个复杂的任务分解为多个子任务，每个子任务由一个"专家"（Expert）网络处理，同时通过一个门控（Gating）网络来决定对于每个输入应该激活哪些专家。

一个简单的MOE结构包含：

  • N个专家网络（通常是相同结构的神经网络）

  • 1个门控网络（负责选择激活哪些专家）

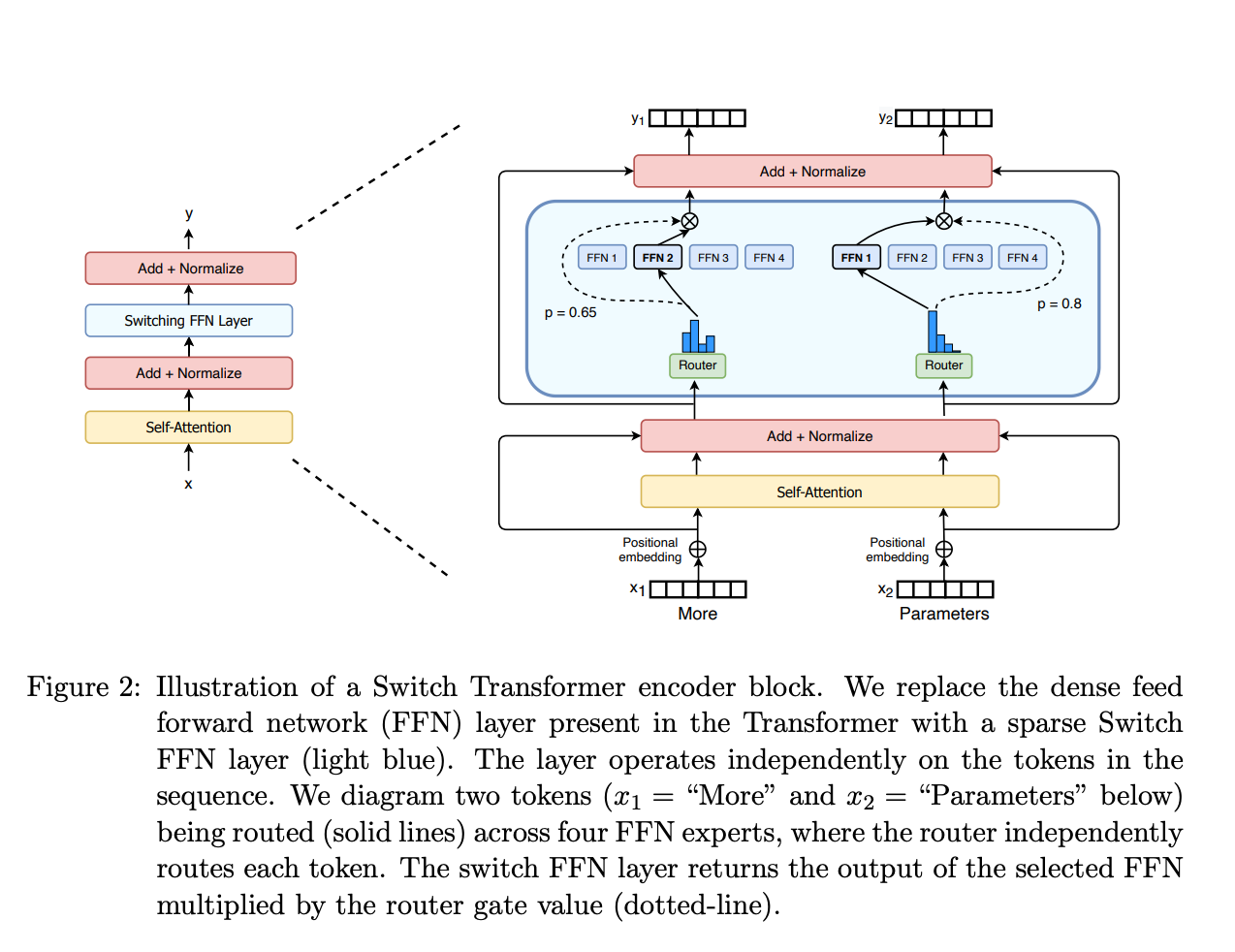
对于每个输入样本，门控网络会生成一个权重分布，通常只选择权重最高的K个专家进行激活（这就是"稀疏"的来源），然后将这些专家的输出加权组合得到最终结果。

2. 参数量计算#

首先，让我们来分析MOE模型的参数量。假设我们有：

  • N个专家网络，每个专家的参数量为E

  • 1个门控网络，参数量为G

那么MOE模型的总参数量为：

总参数量 = N × E + G

这个公式很直观：所有专家的参数加上门控网络的参数。与同等参数量的密集模型相比，MOE可以拥有更多的总参数，但实际计算时只使用其中的一部分。

让我们用代码来实现一个简单的参数量计算：

def calculate_moe_parameters(num_experts, expert_params, gate_params):
    """
    计算MOE模型的总参数量
    
    参数:
        num_experts: 专家网络的数量
        expert_params: 单个专家网络的参数量
        gate_params: 门控网络的参数量
        
    返回:
        total_params: MOE模型的总参数量
    """
    total_params = num_experts * expert_params + gate_params
    return total_params

现在，让我们用一个例子来计算：

# 假设我们有8个专家，每个专家有1000万个参数
# 门控网络有100万个参数
num_experts = 8
expert_params = 10_000_000  # 10M
gate_params = 1_000_000     # 1M

moe_total_params = calculate_moe_parameters(num_experts, expert_params, gate_params)
print(f"MOE模型总参数量: {moe_total_params:,}")

# 对比一个参数量相近的密集模型
dense_model_params = 25_000_000  # 25M
print(f"密集模型参数量: {dense_model_params:,}")

从上面的计算可以看出，MOE模型可以拥有比同计算量的密集模型多得多的参数，这也是MOE能够在保持计算效率的同时提升模型能力的关键。

计算量（通常用FLOPs，即浮点运算次数来衡量）的评估要比参数量复杂一些，因为它不仅取决于模型结构，还与输入数据和激活的专家数量有关。

3. 推理阶段计算量#

在推理阶段，对于每个输入样本，MOE模型只会激活一部分专家（通常是固定数量K的专家）。因此，推理阶段的计算量为：

推理计算量 = K × E_flops + G_flops

其中：

  • K是每次激活的专家数量

  • E_flops是单个专家处理一个样本的计算量

  • G_flops是门控网络处理一个样本的计算量

让我们实现推理计算量的评估函数：

def calculate_inference_flops(num_active_experts, expert_flops_per_sample, gate_flops_per_sample):
    """
    计算MOE模型在推理阶段的计算量
    
    参数:
        num_active_experts: 每次推理激活的专家数量
        expert_flops_per_sample: 单个专家处理一个样本的FLOPs
        gate_flops_per_sample: 门控网络处理一个样本的FLOPs
        
    返回:
        inference_flops: 推理阶段的总FLOPs
    """
    inference_flops = num_active_experts * expert_flops_per_sample + gate_flops_per_sample
    return inference_flops

4. 训练阶段计算量#

训练阶段的计算量要复杂一些，主要有两个原因：

  1. 为了计算专家的梯度，我们需要保留所有被激活专家的中间结果

  2. 门控网络的训练也需要额外计算

在训练阶段，对于每个输入样本，计算量为：

训练计算量 = K × (E_flops + E_backward_flops) + (G_flops + G_backward_flops)

其中，带_backward后缀的项表示反向传播的计算量。在简化情况下，我们可以假设反向传播的计算量大约是前向传播的2倍，因此：

训练计算量 ≈ K × 3 × E_flops + 3 × G_flops

让我们实现训练计算量的评估函数：

def calculate_training_flops(num_active_experts, expert_flops_per_sample, gate_flops_per_sample):
    """
    计算MOE模型在训练阶段的计算量
    
    参数:
        num_active_experts: 每次训练激活的专家数量
        expert_flops_per_sample: 单个专家处理一个样本的FLOPs
        gate_flops_per_sample: 门控网络处理一个样本的FLOPs
        
    返回:
        training_flops: 训练阶段的总FLOPs（包含反向传播）
    """
    # 简化假设：反向传播计算量是前向传播的2倍
    expert_total = expert_flops_per_sample * 3  # 1倍前向 + 2倍反向
    gate_total = gate_flops_per_sample * 3      # 1倍前向 + 2倍反向
    
    training_flops = num_active_experts * expert_total + gate_total
    return training_flops

5. 实验对比与分析#

现在，让我们通过一个完整的例子来对比MOE模型和密集模型在参数量和计算量上的差异：

# 模型参数设置
num_experts = 8        # 专家数量
expert_params = 10_000_000  # 每个专家的参数量
gate_params = 1_000_000     # 门控网络参数量
num_active_experts = 2  # 每次激活的专家数量

# 计算量参数（每个样本）
expert_flops = 50_000_000   # 单个专家前向计算量
gate_flops = 2_000_000      # 门控网络前向计算量

# 计算MOE模型的参数量
moe_params = calculate_moe_parameters(num_experts, expert_params, gate_params)

# 计算MOE模型的计算量
moe_inference_flops = calculate_inference_flops(num_active_experts, expert_flops, gate_flops)
moe_training_flops = calculate_training_flops(num_active_experts, expert_flops, gate_flops)

# 对比的密集模型（与MOE推理计算量相近）
# 我们计算一个与MOE推理计算量相近的密集模型
dense_model_flops = moe_inference_flops
# 假设密集模型的参数与计算量比例和专家网络相似
dense_model_params = (dense_model_flops / expert_flops) * expert_params

print(f"MOE模型总参数量: {moe_params:,}")
print(f"对比密集模型参数量: {int(dense_model_params):,}")
print(f"MOE参数量是密集模型的 {moe_params / dense_model_params:.2f} 倍")
print()
print(f"MOE推理计算量: {moe_inference_flops:,} FLOPs/样本")
print(f"MOE训练计算量: {moe_training_flops:,} FLOPs/样本")
print(f"训练计算量是推理的 {moe_training_flops / moe_inference_flops:.2f} 倍")

从上面的实验结果可以看出：

  1. MOE模型可以在保持推理计算量与密集模型相当的情况下，拥有多得多的参数量（通常是数倍）

  2. 训练计算量大约是推理计算量的3倍左右（这与我们的理论假设一致）

6. 批处理下计算量#

在实际应用中，我们通常会批处理多个样本。这时候，MOE模型的计算效率优势会更加明显。

让我们扩展一下我们的计算函数，考虑批处理的情况：

def calculate_batch_inference_flops(batch_size, num_active_experts, expert_flops_per_sample, gate_flops_per_sample):
    """计算批处理情况下MOE模型的推理计算量"""
    # 专家计算可以高效地批处理
    expert_flops = num_active_experts * expert_flops_per_sample * batch_size
    # 门控网络也需要处理每个样本
    gate_flops = gate_flops_per_sample * batch_size
    return expert_flops + gate_flops

# 计算批次大小为32时的情况
batch_size = 32
batch_inference_flops = calculate_batch_inference_flops(batch_size, num_active_experts, expert_flops, gate_flops)
print(f"批处理推理计算量 ({batch_size}样本): {batch_inference_flops:,} FLOPs")
print(f"平均每个样本: {batch_inference_flops / batch_size:,} FLOPs")

批处理情况下，每个样本的平均计算量与单个样本的计算量基本一致，这表明MOE模型在批处理场景下同样保持高效。

7. 总结与思考#

参数量主要由专家数量 \(N\)、单个专家参数量 \(E\) 和门控网络参数量 \(G\) 共同决定，总参数量为 \(N \times E + G\)，这使得 MOE 能在控制计算量的同时拥有远超同计算密集模型的参数量。

计算量在推理阶段与激活的专家数量 \(K\) 成正比，公式为 \(K×E_{flops} + G_{flops}\)，这种稀疏激活机制让大参数模型保持高效推理；而训练阶段因包含反向传播，计算量约为推理阶段的 \(N\) 倍，体现了训练与推理的显著差异。

训练时的计算与显存消耗，受激活专家数量 \(K\) 和单个专家的前反向计算量共同影响，所有被激活专家的中间结果都需保留，这是训练成本的主要来源。推理时的效率则源于稀疏激活特性，仅处理 \(K\) 个专家的计算，配合门控网络的选择机制，在保持模型能力的同时大幅降低了实际计算负担，这也是 MOE 能在大模型领域广泛应用的核心优势。

本节目录 Contents