Ring Attention#
Author by: 付溦崴
Ring Attention 将一段序列放到多张卡上进行计算，每张卡保存 \(Q\)、\(K\)、\(V\) 矩阵的一部分，通过环状通信在多卡之间发送/接受新的 \(K\)、\(V\) 矩阵 block，达到更新注意力输出的目的。Ring Attention 除了对 Attention 进行多卡分块计算，还将 FFN 层进行多卡分块计算，因此 Ring Attention 本质上就是分布式版本的 BPT（Blockwisew Parallel Transformers），可以简单地将两者与 Flash Attention2 的关系理解为：Flash Attention2->BPT(Flash Attention2 + 分块 MLP)->Ring Attention(分布式版本的 BPT)。
Attention 分块计算#
我们假设 \(Q\)、\(K\)、\(V\) 矩阵的尺寸均为（N，d），其中 N=seq_len，d=hidden_size，为简单起见，我们将序列切分为 4 个 chunk（假设我们有 4 张卡，每张卡负责一个 chunk），每个 chunk 大小为（C，d），如下图所示：
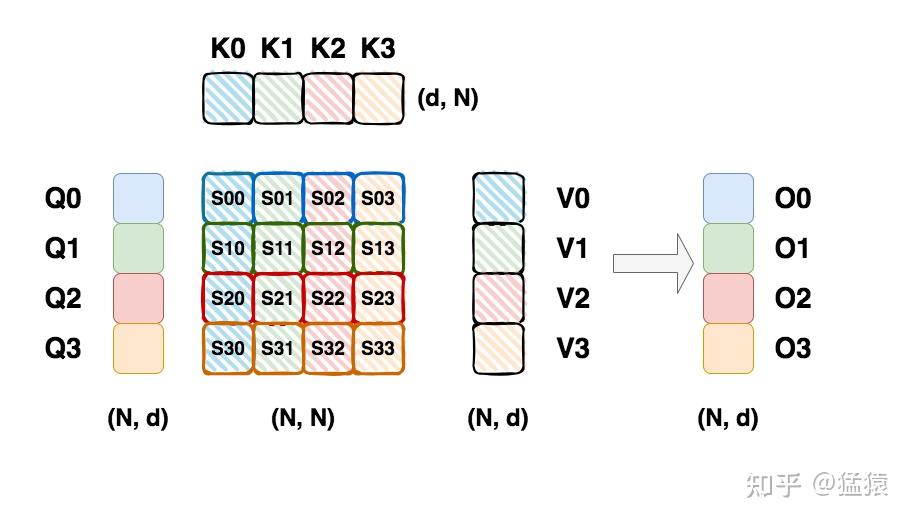
每个块的注意力输出 \(O_i\) 需要用到 \(Q_i\) 矩阵（1 个 chunk）和所有的 \(K\) 矩阵和 \(V\) 矩阵（所有 chunk），因此在多卡计算的时候每张卡的 \(Q_i\) 是固定的。在每块 GPU 上的计算流程是：
传入 \(K_j\) 以及 \(V_j\)；
计算 \(Q_i\) 与 \(K_j\) 的注意力分数 \(S_{i,j}\)；
计算 \(S_{i,j}\) 与 \(V_j\) 的矩阵乘法，得到 \(O_i^j\)；
传入其他 \(K\)、\(V\) 矩阵的 chunk，重复上述过程，更新得到最后的 \(O_i\)。
上述过程如下图所示：
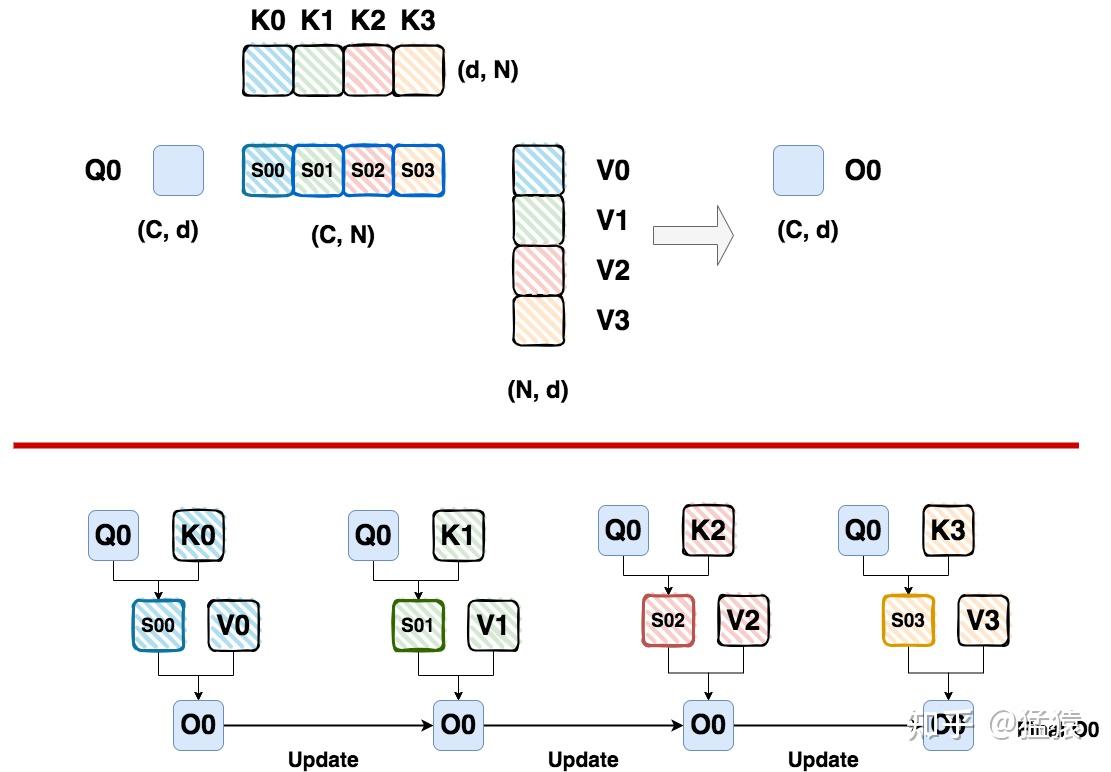
这里需要注意的是 \(O_i\) 是如何更新的。由于注意力机制需要对注意力分数矩阵做 softmax，因此我们需要获得分数矩阵每行的全局最大值以及 sum，记作 global max 和 global sum，但我们在分块计算的过程使用是 local max 以及 local sum。Ring Attention 更新 \(O_i\) 的方式与 Flash Attention2 基本一致。
多 GPU 环状通信#
上面的分块流程已经提及，每次计算得到的 \(O_i^j\) 只需要用到 \(K_j\) 以及 \(V_j\)，因此每张 GPU 仅仅保留对应需要的 chunk，在下一次更新 \(O_i^{j+1}\) 的时候需要从其他卡接收 \(K_{j+1}\) 以及 \(V_{j+1}\)，这样就能够达到节约显存的目的。不过需要注意的是，这个过程会增加通信量，因此需要设计合理的 chunk size，使得计算与通信的时间相互遮盖。下面是环状通信的流程：
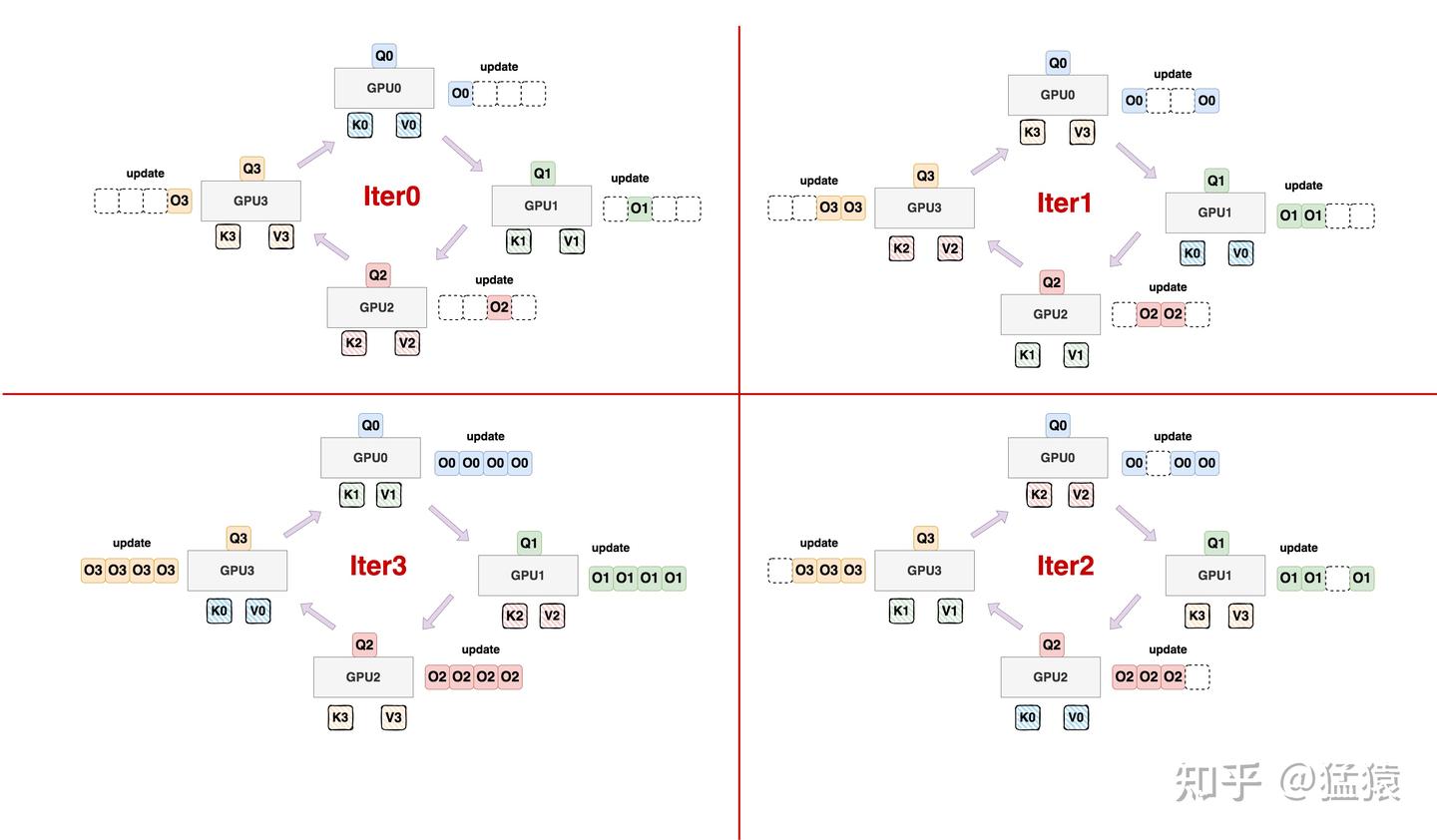
首先将 \(Q\) 分块放置到每张 GPU 内，各卡上的 \(Q\) 分块不变；
接着，每块卡上只放一块 \((K，V)\) 对。也就是每次计算时，哪个 \((K，V)\) 对需要被这块卡用到，哪个 \((K，V)\) 对就在这块卡上放着。初始化的状态如图 iter0 所示；
接着，在每块卡使用当前 \((K，V)\) 对做 Attention 计算时:
接收来自前一块卡的 \((K，V)\) 对，并把自己当前维护的 \((K，V)\) 对发给下一张卡，形成一个环状通信拓扑
例如，当 GPU0 正在使用 \((K_0，V_0)\) 进行计算时，它接收来自 GPU3 的 \((K_3，V_3)\) ，同时把自己的 \((K_0，V_0)\) 发送给 GPU1，其余卡也是类推。
在我们的图中，为了更好表示这一个更新过程，对于某个 \(O_i\) 我们画出了若干个，但正如上文所说，实际运行时我们只维护一个 \(O_i\) 并不断更新它。这里画出多个 \(O_i\) 只是更好帮助大家理解。
显存分析#
这里不考虑 FFN 层分块的影响，仅对 Attention 显存占用进行分析，精度假设为 bf16：每张卡需要保存一个 \(Q_i\)，\(K_j\)，\(V_j\) 来计算当前的 \(O_i^j\)，占用 6Cd bytes；还需要保存获取从前一张 GPU 上获取的 \(K_{j-1}\)、\(V_{j-1}\) 占用 4Cd bytes；计算更新过程中需要保存当前的 \(O_i^j\) 占用 2Cd bytes，因此总共占用 12Cd bytes。
Chunk Size 设置#
为了不影响效率，设置的原则是【传输时间 <= 计算时间】，这样才可以让这部分开销被计算覆盖住，进而不影响整个系统的计算效率。而要做到这一点，就需要我们根据所使用的卡的配置，设计好最优的分块大小，也就是上图中所说的 C（chunk size），用于表示一个分块中包含多长的序列。为了表达简便，我们在做各种指标计算时忽略掉 batch_size 维度。
我们假设：
硬件（例如单张 GPU）的算力上限是 F，单位是 FLOPS 或者 FLOP/s。
硬件的带宽上限是 B，单位是 Byte/s。
单卡在对每个 chunk 进行计算的时候，计算 Attention score 的计算量为 \(2dC^2\) FLOPs，Attention score 与 \(V\) 矩阵相乘的计算量为 \(2dC^2\) FLOPs，因此 Attention score 的整体计算量为 \(4dC^2\) FLOPs。
传输数据（\(K\)，\(V\) 分块）的通信总量为 \(4dC\) bytes。根据【传输时间<=计算时间】的基本要求，我们有： \(\frac{4dC}{B} \leq \frac{4dC^2}{F}\)，进一步可得：\(C \geq \frac{F}{B}\)，及我们根据硬件的算力和带宽得到的最优切块大小。
上面的推导过程中没有考虑 \(W_Q\)，\(W_K\)，\(W_V\) 矩阵的映射的计算量，因此对 \(C\) 的要求也是更严格的，因为这意味着要求在 Attention Score 的计算量下完成通信，而不是在实际情况 Attention score + Projection 的计算量下完成通信。
Ulysses 长序列并行#
Hybrid Attention#
参考链接：
Ring Attention with Blockwise Transformers for Near-Infinite Context