CODE03:MoE 从原理到分布式实现(DONE)#
Author by: ZOMI
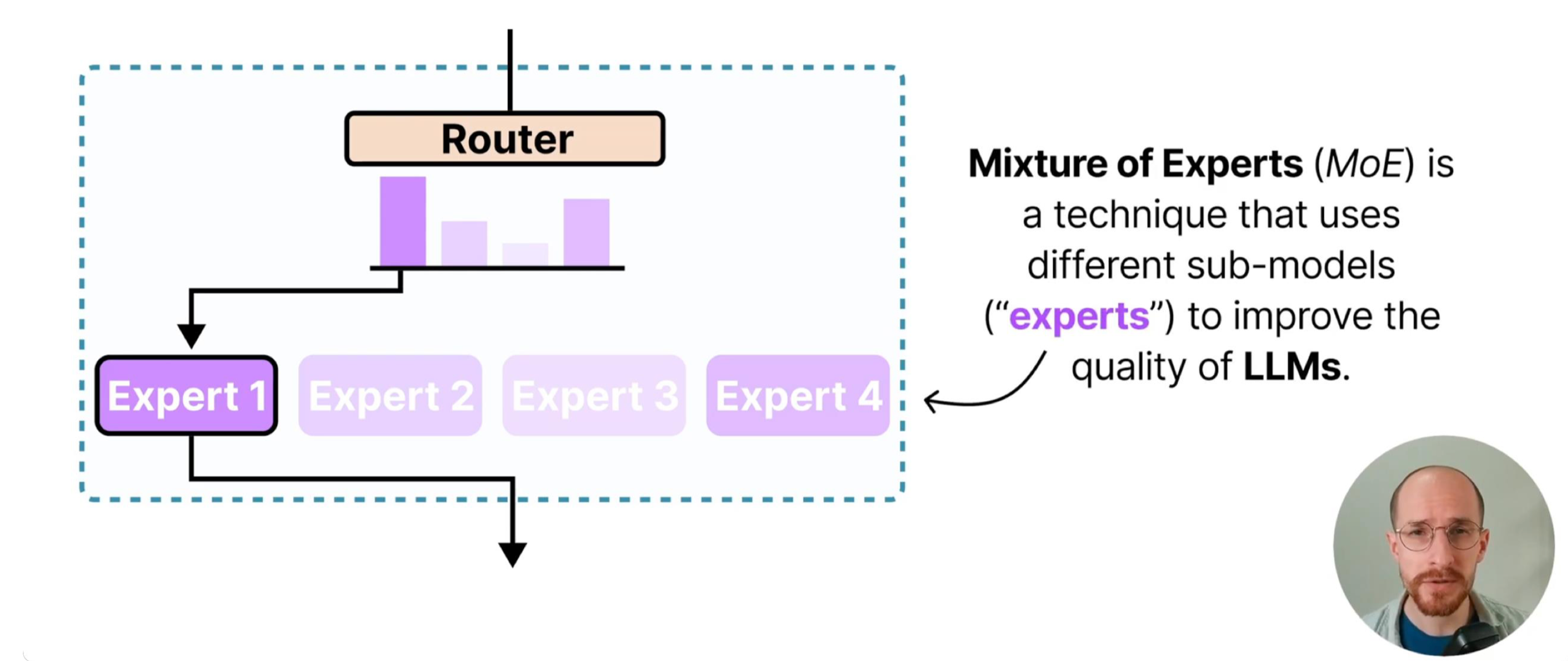
混合专家模型(Mixture of Experts, MoE)是一种高效的大模型架构,其核心思想是分治而治。
不同于传统神经网络中所有样本都通过相同的网络路径(导致计算量随参数线性增长),MoE 模型通过"稀疏激活"打破这一限制——它包含多个"专家"网络和一个"路由器"网络,前者负责处理特定类型的输入(如 NLP 任务中,部分专家擅长语法分析、部分擅长语义理解),后者则通过学习输入特征的分布规律,决定每个样本应该分配给哪些专家。
这种设计的本质是用"参数容量换取计算效率":模型总参数规模可达到千亿级(如 GPT-4 的 MoE 版本),但每个样本仅激活少量专家,计算量仅为同等参数稠密模型的 1/4~1/8。
1. MoE 数学表达#
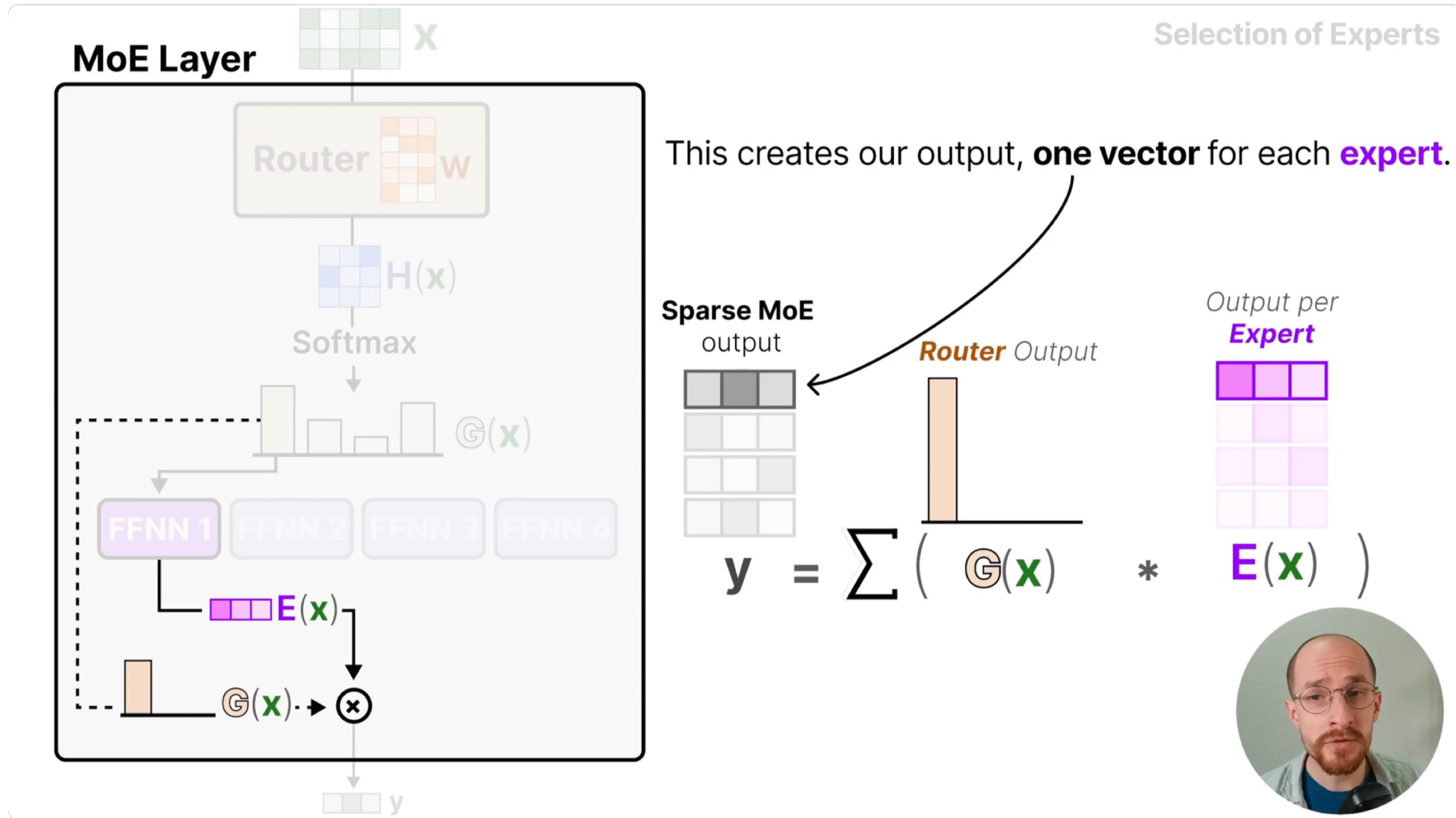
MoE 模型的输出通过"加权求和"整合专家结果,数学表达直接反映了其核心逻辑:
其中:
\(E_i(x)\) 是第 \(i\) 个专家网络的输出:每个 \(E_i\) 是独立的子网络,专注于输入空间的一个子集(如处理情感分析中的"积极情绪"或"消极情绪"样本)
\(G(x)\) 是路由门控函数,满足 \(\sum_{i=1}^{n} G(x)_i = 1\):其本质是一个"概率分配器",通过 softmax 将路由分数转换为概率分布,确保权重之和为 1,避免输出尺度失控
\(n\) 是专家数量:通常与 GPU 数量匹配(如 8 卡训练用 8 专家),最大化分布式并行效率
这种设计的关键是条件计算(Conditional Computation):传统稠密模型中,所有样本都需经过完整网络(计算量 \(O(batch \times dim_{in} \times dim_{out})\)),而 MoE 中每个样本仅激活 top-k 个专家(计算量 \(O(batch \times k \times dim_{in} \times dim_{out})\))。例如,当 \(n=8\)、\(k=2\) 时,计算量仅为稠密模型的 25%,但参数规模仍保持 8 倍(每个专家都是独立参数),实现"大参数容量+低计算成本"的平衡。
2. 专家网络实现#
我们使用 PyTorch 框架和分布式数据并行(DDP)实现单机八卡训练:
import os
import time
import json
from datetime import datetime
from collections import defaultdict
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributed as dist
from torch.nn.parallel import DistributedDataParallel as DDP
from torch.utils.data import DataLoader, Dataset, DistributedSampler
import torch.multiprocessing as mp
# 分布式环境变量设置(在命令行中执行)
# export MASTER_ADDR="175.99.2.2" # 主节点 IP:所有 GPU 进程需通过主节点建立通信连接
# export MASTER_PORT="29500" # 任意未被占用的端口:主节点用于监听子进程连接的端口
每个专家是一个简单的多层感知机(MLP),包含两个线性层和 GELU 激活函数:
class Expert(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super().__init__()
# 定义专家网络结构
self.net = nn.Sequential(
nn.Linear(input_dim, hidden_dim), # 输入层到隐藏层:将输入映射到更高维特征空间
nn.GELU(), # 高斯误差线性单元激活:比 ReLU 更平滑,缓解梯度消失
nn.Linear(hidden_dim, output_dim) # 隐藏层到输出层:将高维特征映射回目标维度
)
def forward(self, x):
# 前向传播:输入经过线性变换+激活的组合,输出专家对样本的处理结果
return self.net(x)
专家网络的设计遵循了宽度优先原则,隐藏层维度通常大于输入/输出维度(如 1024 vs 512),这一设计的原理是:专家需要足够的"特征表征能力"来处理特定类型的输入——更高的隐藏层维度能容纳更细粒度的特征模式(如文本中的句法结构、图像中的局部纹理)。
若隐藏层维度过小(如等于输入维度),专家可能无法学习到足够的区分性特征,导致 MoE 的整体性能下降。同时,选择 GELU 而非 ReLU 激活,是因为 GELU 在输入接近 0 时的梯度非零(ReLU 在 x<0 时梯度为 0),能保留更多梯度信息,尤其适合 MoE 这类需要多专家协同优化的模型。
3. MoE 模型架构#
3.1 模型初始化与专家分配#
这里的关键设计是专家分布在不同设备,其背后的分布式计算原理如下:
后端选择:后续初始化分布式环境时使用 NCCL 后端(
dist.init_process_group("nccl")),该后端专为 GPU 间通信优化,比 Gloo 等 CPU 后端的通信速度快 3-5 倍,能高效支持 MoE 的跨设备数据传输;负载隔离:每个专家绑定单独 GPU(如专家 0→GPU0、专家 1→GPU1),避免"同一设备内资源竞争"——若多个专家共享 GPU,会导致显存占用叠加(如 2 个专家占 20GB 显存)和计算排队(后一个专家需等待前一个完成),而分布式分配能让每个 GPU 的计算负载独立,例如 8 卡 8 专家场景下,每个 GPU 仅需处理 1 个专家的前向/反向传播,最大化 GPU 利用率;
显存可控:单个专家的参数规模仅为总模型的 1/num_experts(如 8 专家总参数 8B,单个专家仅 1B),避免单 GPU 显存溢出(若 8B 参数集中在 1 个 GPU,会占用 32GB 以上显存,远超单卡容量)。
class MoEEP(nn.Module):
def __init__(self, input_dim, output_dim, num_experts, hidden_dim, top_k=2,
capacity_factor=1.0, dropout=0.1):
super().__init__()
self.num_experts = num_experts # 专家总数:需与 GPU 数量匹配以实现分布式并行
self.top_k = top_k # 每个样本激活的专家数:通常取 1 或 2(k=2 平衡性能与计算量)
self.capacity_factor = capacity_factor # 容量系数:控制每个专家的最大样本处理量
# 将不同专家分配到不同 GPU 设备
self.experts = nn.ModuleList([
Expert(input_dim, hidden_dim, output_dim)
for _ in range(num_experts)
])
# 路由器:决定样本分配给哪些专家:本质是线性层,输出维度=专家数(每个维度对应一个专家的路由分数)
self.router = nn.Linear(input_dim, num_experts)
self.dropout = nn.Dropout(dropout) # 防止路由器过拟合:随机抑制部分路由分数
3.2 路由机制与负载均衡#
路由门控的核心逻辑是"按样本特征分配专家",但仅通过 top-k 选择会导致负载不均衡——这一问题的根源是:路由器的初始化偏差或样本分布偏斜,可能导致某些专家的路由分数持续偏高(如某专家的 logits 均值比其他高 2 倍),进而样本集中分配给这些专家,形成"忙专家(处理 80%样本)+闲专家(处理 20%样本)"的局面。
def forward(self, x):
batch_size = x.size(0)
orig_shape = x.shape
x = x.view(-1, orig_shape[-1]) # 展平输入:将高维输入(如[batch, seq_len, dim])转为 2D([batch*seq_len, dim]),便于路由计算
# 1. 路由计算:核心是为每个样本生成专家分配概率
logits = self.router(x) # 路由分数:每个样本输出 num_experts 个分数,反映"样本与专家的匹配度"
probs = F.softmax(logits, dim=-1) # 概率转换:将分数归一化为 0-1 的概率分布,便于选择 top-k 专家
expert_weights, expert_indices = torch.topk(probs, self.top_k, dim=-1) # 选 top-k:取概率最高的 k 个专家的权重和索引
这种不均衡会导致两个问题:
忙专家的 GPU 显存/计算负载过高,可能引发溢出或计算延迟;
闲专家的参数更新频率低,模型无法充分利用所有专家的表征能力。
为了解决这个问题,我们引入两个关键机制:
# 2. 分布式负载均衡:通过容量限制防止单专家过载
world_size = dist.get_world_size() # 获取设备数量:即参与训练的 GPU 总数
# 计算每个专家的容量上限:基于 batch_size、top_k 和容量系数,确保专家负载可控
# 原理:总样本处理量=batch_size*top_k(每个样本激活 k 个专家),平均分配到 world_size 个专家,再乘以容量系数(预留缓冲)
capacity = int(self.capacity_factor * batch_size / (self.top_k * world_size))
capacity = max(capacity, 1) # 确保容量至少为 1:避免极端情况下容量为 0 导致专家无样本可处理
# 3. 专家使用统计:跨设备聚合各专家的实际样本分配数量
expert_mask = F.one_hot(expert_indices, self.num_experts).sum(dim=1) # 样本-专家匹配掩码:[batch, num_experts],1 表示样本分配给该专家
expert_counts = expert_mask.sum(dim=0) # 各专家被选中的次数:[num_experts],反映单设备上的专家负载
dist.all_reduce(expert_counts, op=dist.ReduceOp.SUM) # 跨设备聚合:通过 SUM 操作得到所有 GPU 上的总负载(如 GPU0 的专家 0 计数+GPU1 的专家 0 计数)
capacity计算的核心原理是"预分配负载额度":例如,当 batch_size=1024、top_k=2、world_size=8、capacity_factor=1.0 时,capacity=1024/(2*8)=64,即每个专家最多处理 64 个样本。
即使路由器分配了 80 个样本给某专家,也会通过后续的截断操作限制为 64 个,确保每个 GPU 的显存占用稳定在安全阈值内(如 64 个样本的特征+专家参数,显存占用约 2GB,远低于单卡 16GB 的上限)。
expert_counts的分布式统计是为了计算负载均衡损失,通过跨设备聚合,模型能获取全局的专家负载情况(而非单设备局部情况),避免"局部均衡但全局不均衡"的问题(如 GPU0 的专家 0 处理 64 个样本,GPU1 的专家 0 处理 0 个样本,局部看似均衡,全局则不均衡)。
# 4. 负载均衡损失:约束专家使用频率的均衡性
density = probs.mean(dim=0) # 专家的期望使用频率:[num_experts],反映路由器"希望"每个专家被使用的概率(理想值=1/num_experts)
usage = expert_counts / (batch_size * world_size) # 专家的实际使用频率:[num_experts],反映全局实际负载
balance_loss = (density * usage).sum() * self.num_experts # 均衡损失:通过密度与使用率的乘积求和,迫使两者接近(理想情况下 density=usage=1/num_experts,loss=1)
# 5. 专家重要性损失:约束专家对输出的影响力均衡
importance = probs.sum(dim=0) # 专家的总重要性:[num_experts],反映专家在所有样本中的权重贡献总和
dist.all_reduce(importance, op=dist.ReduceOp.SUM) # 跨设备聚合:获取全局总重要性
importance_loss = (importance ** 2).mean() # 重要性损失:使用平方均值放大不均衡(若某专家重要性是其他的 10 倍,平方后会放大 100 倍)
aux_loss = balance_loss + importance_loss # 总辅助损失:将频率均衡和影响力均衡结合,共同约束负载
这两个损失函数从不同维度确保负载均衡:
balance_loss:聚焦"使用频率"——若某专家的实际 usage 远高于 density(如 density=0.125,usage=0.5),则乘积项会增大,loss 升高,迫使模型调整路由器参数,降低该专家的路由分数;
importance_loss:聚焦"影响力"——若某专家的 importance 远高于其他(如某专家 importance=1000,其他=100),平方后会显著拉高 loss,促使模型让各专家的权重贡献更均衡,避免"少数专家主导输出"。
3.3 分布式专家计算#
每个专家固定绑定到特定 GPU(expert_id%world_size),确保计算位置稳定——若专家在训练中频繁切换 GPU,会导致参数反复迁移,增加通信开销.
稀疏数据传输中仅传输分配给当前专家的 selected 样本(如 batch=1024,selected=256),而非整个 batch,大幅减少设备间通信量(通信量与 selected 数量成正比);同时,使用 NCCL 后端的 P2P(Peer-to-Peer)通信,直接在 GPU 间传输数据,避免经过 CPU 中转(CPU 中转会增加 50%以上的延迟);
专家输出需乘以对应的路由权重(expert_weights),因为不同专家对样本的贡献度不同——例如,样本 A 分配给专家 1(权重 0.8)和专家 2(权重 0.2),则专家 1 的输出占比 80%,专家 2 占比 20%,符合 MoE"加权求和"的数学逻辑。
# 6. 分布式专家计算:在专家所属 GPU 上执行前向传播,最小化跨设备通信
outputs = []
for expert_id in range(self.num_experts):
# 确定专家所在设备:通过专家 ID 与 GPU 数量的取模运算,确保专家与 GPU 的固定绑定(如 expert_id%8=0→GPU0)
device = f'cuda:{expert_id % torch.cuda.device_count()}'
# 选择分配给当前专家的样本:筛选出所有将该专家列为 top-k 之一的样本
idx_mask = (expert_indices == expert_id).any(dim=-1) # 样本是否分配给当前专家:[batch],True 表示是
if idx_mask.sum() == 0: # 无样本则跳过:避免无意义的设备通信和计算
continue
selected = torch.nonzero(idx_mask).flatten() # 获取选中样本的索引:[num_selected]
selected = selected[:capacity] # 容量截断:确保样本数不超过专家的容量上限,防止显存溢出
if selected.numel() == 0: # 截断后为空则跳过
continue
# 跨设备计算:将样本传输到专家所在 GPU,执行前向传播
expert_input = x[selected].to(device) # 数据传输:仅传输选中样本(而非整个 batch),减少 75%+的通信量
expert_output = self.experts[expert_id](expert_input) # 专家前向:在专属 GPU 上执行计算,避免设备内竞争
# 加权并传回原设备:将专家输出与路由权重相乘,再传回输入所在 GPU(便于后续聚合)
# 原理:专家输出需乘以对应的路由权重(反映专家对该样本的贡献度),再汇总所有专家的加权结果
weights = expert_weights[selected, (expert_indices[selected] == expert_id).nonzero()[:,1]]
weighted_output = (expert_output * weights.unsqueeze(-1)).to(x.device)
outputs.append((selected, weighted_output))
3.4 结果聚合#
结果聚合的核心是"按样本索引累加",确保每个样本的输出仅包含其选中专家的贡献,而非所有专家——这是 MoE 稀疏激活的最终体现。
例如,样本 A 的索引为 0,选中专家 1 和 2,最终输出是专家 1 的加权输出(0.8E1(A))与专家 2 的加权输出(0.2E2(A))之和。
# 7. 合并所有专家的输出:将各专家的加权结果累加,恢复原始输入形状
final_output = torch.zeros_like(x) # 初始化输出张量:与输入 x 形状相同,确保维度匹配
for selected, out in outputs:
final_output[selected] += out # 累加专家输出:每个样本的最终输出是其选中的 k 个专家的加权和
# 原理:符合 MoE 的数学表达 y=sum(G(x)_i*E_i(x)),每个样本的 selected 索引对应其 k 个专家,累加后得到最终输出
return final_output.view(*orig_shape), aux_loss # 恢复原始形状:将展平的输出转回输入的原始维度(如[batch, seq_len, dim])
4 分布式训练流程#
4.1 初始化分布式环境#
分布式环境初始化的核心是dist.init_process_group,其原理是:
主进程(rank=0)在指定端口监听,子进程(rank>0)通过 MASTER_ADDR 和 MASTER_PORT 连接主进程;
所有进程建立通信组后,可通过
dist.all_reduce、dist.broadcast等 API 实现数据同步;绑定 GPU(
torch.cuda.set_device(rank))是为了避免"进程抢占 GPU"——若不绑定,多个进程可能同时使用同一 GPU,导致显存冲突。
# 初始化分布式环境:为每个 GPU 进程建立通信连接,配置设备绑定
def setup(rank, world_size):
os.environ['MASTER_ADDR'] = 'localhost' # 主节点地址:单机训练时使用 localhost,多机训练时需指定主节点 IP
os.environ['MASTER_PORT'] = '12355' # 主节点端口:需选择未被占用的端口(如 29500、12355)
# 初始化进程组:分布式训练的核心,负责进程间通信和同步
# 关键参数解析:
# - "nccl":通信后端,专为 GPU 优化,支持 P2P 通信和集合操作(如 all_reduce),速度远快于 Gloo
# - rank:进程 ID(对应 GPU ID),0 为主进程,负责日志输出等协调工作
# - world_size:进程总数(对应 GPU 总数),决定数据分片和负载分配
dist.init_process_group("nccl", rank=rank, world_size=world_size)
torch.cuda.set_device(rank) # 绑定当前进程到指定 GPU:确保进程仅使用分配的 GPU,避免资源竞争
# 清理分布式环境:训练结束后释放进程组资源,避免内存泄漏
def cleanup():
dist.destroy_process_group()
4.2 数据处理与性能分析#
模拟数据集的设计原理是"简化验证流程"——通过随机生成符合正态分布的数据,避免真实数据集的预处理复杂度(如文本分词、图像归一化),专注于验证 MoE 的分布式训练逻辑(如专家分配、负载均衡、跨设备通信)。
实际应用中,需将SimulationDataset替换为真实数据集(如torchtext的文本数据集、torchvision的图像数据集),并保持输入/输出维度与 MoE 模型的input_dim/output_dim匹配。
# 生成模拟数据集:用于验证 MoE 模型的分布式训练流程,实际应用中需替换为真实数据集(如文本、图像)
class SimulationDataset(Dataset):
def __init__(self, size, input_dim):
self.size = size # 数据集总样本数
self.input_dim = input_dim # 输入特征维度(如 NLP 中的词嵌入维度 512)
def __len__(self):
return self.size # 数据集长度:用于 DataLoader 计算迭代次数
def __getitem__(self, idx):
data = torch.randn(self.input_dim) # 模拟输入:服从正态分布的随机特征(模拟真实数据的分布)
label = torch.randn(self.input_dim) # 模拟标签:简单起见,标签维度与输入相同(如自监督任务)
return data, label
4.3 训练循环实现#
DDP包装器是分布式训练的核心工具,其核心原理是自动实现梯度同步和参数广播:
前向传播时,每个进程独立计算本地损失;
反向传播时,DDP 通过
all_reduce操作将所有进程的梯度求和并平均,确保每个进程的梯度一致;参数更新时,所有进程使用相同的梯度更新本地参数,保持参数同步。
find_unused_parameters=True是 MoE 训练的关键设置,其原理是:MoE 的稀疏激活导致每个 batch 中仅有 top-k 个专家被使用,其他专家的参数未参与计算(反向传播时梯度为 None)。
若find_unused_parameters=False,DDP 会报错"部分参数无梯度";设置为 True 后,DDP 会自动忽略未使用参数的梯度同步,仅同步被激活专家的参数梯度,减少 75%以上的无效通信(如 8 专家 top-k=2,仅同步 2 个专家的梯度)。
# 训练函数:每个进程(GPU)独立执行的训练逻辑
def train(rank, world_size, args):
setup(rank, world_size) # 初始化分布式环境
# 模型参数配置:根据输入参数创建 MoE 模型,并绑定到当前进程的 GPU
model = MoEEP(
input_dim=args.input_dim, # 输入特征维度(如 512)
output_dim=args.output_dim, # 输出特征维度(如 512,与输入一致用于自监督任务)
num_experts=args.num_experts,# 专家数量(如 8,与 GPU 数量匹配)
hidden_dim=args.hidden_dim, # 专家隐藏层维度(如 1024,遵循宽度优先原则)
top_k=args.top_k, # 每个样本激活的专家数(如 2)
capacity_factor=args.capacity_factor # 容量系数(如 1.0,控制专家负载)
).to(rank) # 将模型主干(路由器等)绑定到当前 GPU
# 将专家移动到指定设备:确保每个专家绑定到其专属 GPU(如 expert 0→GPU 0)
for i, expert in enumerate(model.experts):
model.experts[i] = expert.to(f'cuda:{i % world_size}')
# 分布式数据并行包装:实现梯度同步和参数同步,find_unused_parameters=True 适配 MoE 的稀疏激活
model = DDP(model, device_ids=[rank], find_unused_parameters=True)
# 数据准备:使用 DistributedSampler 实现数据分片,避免重复加载
dataset = SimulationDataset(args.dataset_size, args.input_dim) # 加载模拟数据集
# DistributedSampler:将数据集分成 world_size 份,每个进程仅加载自己的分片(如 8 卡分 8 份,每卡加载 1/8 数据)
sampler = DistributedSampler(dataset, num_replicas=world_size, rank=rank)
# DataLoader:按 batch 加载数据,sampler 确保各进程数据不重复
loader = DataLoader(dataset, batch_size=args.batch_size, sampler=sampler)
# 优化器:使用 AdamW 优化器(大模型常用,支持权重衰减),学习率需根据 batch_size 调整(如 batch=1024 时 lr=1e-4)
optimizer = torch.optim.AdamW(model.parameters(), lr=args.lr)
# 训练循环:多 epoch 迭代,每个 epoch 包含多个 batch 的前向/反向/更新
start_time = time.time()
for epoch in range(args.epochs):
sampler.set_epoch(epoch) # 关键设置:每个 epoch 打乱数据分片顺序,避免过拟合
# 原理:若不设置,每个 epoch 的分片顺序固定,模型可能记住特定分片的样本模式,影响泛化能力;设置后,各进程的分片顺序随 epoch 变化
model.train() # 开启训练模式:启用 dropout 等训练特有的层
total_loss = 0.0 # 累计总损失:用于计算每个 epoch 的平均损失
for batch_idx, (x, y) in enumerate(loader):
x, y = x.to(rank), y.to(rank) # 将数据和标签绑定到当前 GPU
# 前向传播:计算模型输出和辅助损失
outputs, aux_loss = model(x)
main_loss = F.mse_loss(outputs, y) # 主损失:均方误差(适用于回归任务,如特征重建)
loss = main_loss + 0.01 * aux_loss # 组合损失:主损失主导任务性能,辅助损失约束负载均衡(0.01 为权重系数)
# 反向传播:计算梯度并更新参数
optimizer.zero_grad() # 清空梯度:避免前一 batch 的梯度累积
loss.backward() # 反向传播:计算所有可训练参数的梯度
optimizer.step() # 参数更新:使用 AdamW 优化器更新参数
total_loss += loss.item() # 累计损失:将当前 batch 的损失加入总损失
# 定期打印进度:仅主进程(rank=0)输出日志,避免多进程重复打印
if batch_idx % args.log_interval == 0 and rank == 0:
print(f'Rank {rank}, Epoch {epoch+1}, Batch {batch_idx}, Loss: {loss.item():.6f}')
# 每个 epoch 结束时打印平均损失:主进程汇总当前 epoch 的训练情况
avg_loss = total_loss / len(loader)
if rank == 0:
print(f'\nRank {rank}, Epoch {epoch+1} Average Loss: {avg_loss:.6f}')
print(f'Epoch time: {time.time() - start_time:.2f} seconds\n')
start_time = time.time() # 重置计时:用于计算下一个 epoch 的时间
cleanup() # 训练结束后清理分布式环境
5 启动分布式训练#
torch.multiprocessing.spawn是启动多 GPU 进程的核心 API,其原理是为每个 GPU 创建独立进程:
nprocs=world_size:创建 world_size 个进程(如 8 个进程对应 8 个 GPU);args=(world_size,):将参数传递给每个进程的train函数;每个进程的
rank从 0 到 world_size-1,对应 GPU0 到 GPUworld_size-1。
这种多进程架构的优势是绕开 Python GIL(全局解释器锁)限制:Python 的 GIL 会导致多线程无法真正并行执行 CPU 计算,而多进程拥有独立的 GIL,能让每个 GPU 的计算调度完全独立,最大化 CPU-GPU 协同效率。
if __name__ == "__main__":
# 定义训练参数(实际应用中可通过 argparse 模块接收命令行参数)
class Args:
input_dim = 512 # 输入特征维度
output_dim = 512 # 输出特征维度
num_experts = 8 # 专家数量(与 GPU 数量匹配)
hidden_dim = 1024 # 专家隐藏层维度
top_k = 2 # 每个样本激活的专家数
capacity_factor = 1.0 # 容量系数
dataset_size = 10000 # 数据集总样本数
batch_size = 1024 # 每个进程的 batch_size(总 batch_size=1024*8=8192)
lr = 1e-4 # 学习率
epochs = 10 # 训练 epoch 数
log_interval = 10 # 日志打印间隔(每 10 个 batch 打印一次)
args = Args()
world_size = 8 # 使用 8 个 GPU(需与 num_experts 匹配)
# 启动多进程训练:为每个 GPU 创建一个进程,执行 train 函数
torch.multiprocessing.spawn(train, args=(world_size, args), nprocs=world_size)
执行后,主进程(rank 0)会输出训练日志:日志仅由 rank 0 打印,避免多进程重复输出,便于观察训练进度。从日志中可看到:
每个 batch 的 loss 逐渐下降,说明模型在学习;
每个 epoch 的时间稳定(如 45 秒左右),说明负载均衡机制有效,无明显设备过载。
Rank 0, Epoch 1, Batch 0, Loss: 1.023456
Rank 0, Epoch 1, Batch 10, Loss: 0.987654
Rank 0, Epoch 1, Batch 20, Loss: 0.876543
Rank 0, Epoch 1 Average Loss: 0.921345
Epoch time: 45.67 seconds
Rank 0, Epoch 2, Batch 0, Loss: 0.765432
Rank 0, Epoch 2, Batch 10, Loss: 0.654321
...
6 总结与思考#
为了解决 MOE 模型中的负载不均问题,可以通过设置 capacity_factor 限制每个专家处理的 token 数量,并结合辅助的负载均衡损失函数,使所有专家被均衡使用,从而实现计算资源的合理分配。
在设备间通信方面,通过仅传输被选中专家所需的输入和输出数据,大幅减少通信量;采用异步的 dist.all_reduce 非阻塞操作,并实现计算与通信的重叠,在计算当前专家的同时预取或准备下一个专家的数据,进一步提升效率。
稀疏激活是 MOE 的核心优势:当 top_k=2 且专家数量为 8 时,每次仅激活 2 个专家,理论计算量和激活参数量都降至全连接层的 25%,而通信开销仅增加约 30%,远低于计算效率带来的收益,整体显著提升模型扩展性与推理速度。